LeetCode题解-009

• 记录LeetCode题目笔记，汇总LeetCode解答记录

Changelog

• 2020/06/14，撰写
• 2020/06/15，添加 LeetCode-14. 最长公共前缀
• 2020/06/15，整理完成

Overview

• LeetCode-1480. 一维数组的动态和
• LeetCode-54. 螺旋矩阵
• LeetCode-59. 螺旋矩阵 II
• LeetCode-14. 最长公共前缀
• LeetCode-1300. 转变数组后最接近目标值的数组和

1480. 一维数组的动态和

Description

• LeetCode-1480. 一维数组的动态和

Approach 1-常规求解

Analysis

本题较简单，不再赘述。

可以直接在原来数组上计算修改。

Solution

• Java

class Solution {
    public int[] runningSum(int[] nums) {
        for(int i=1;i<nums.length;i++){
            nums[i] += nums[i-1];
        }
        return nums;
    }
}

54. 螺旋矩阵

Description

• LeetCode-54. 螺旋矩阵

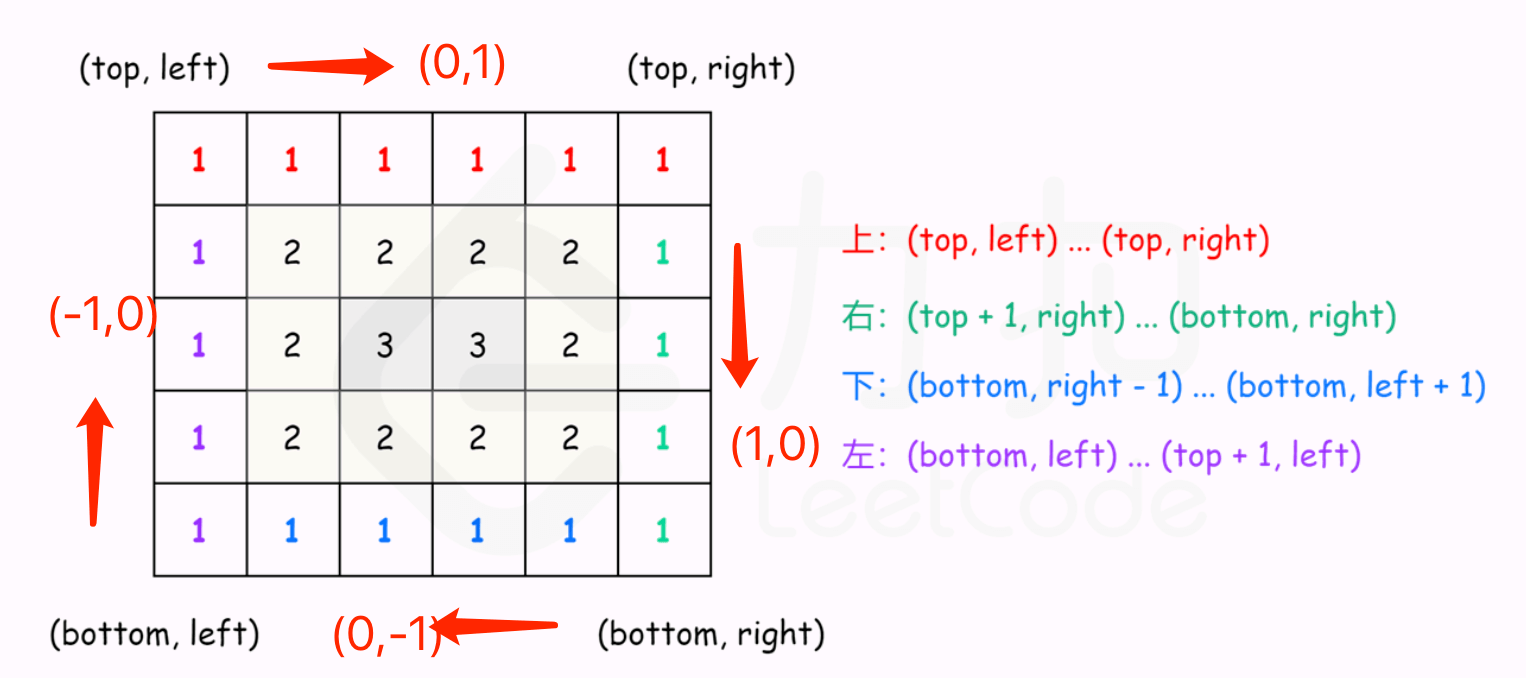
Approach 1-模拟

Analysis

模拟螺旋矩阵的路径。初始位置是矩阵的左上角，初始方向是向右，当路径超出界限或者进入之前访问过的位置时，则顺时针旋转，进入下一个方向。

判断路径是否进入之前访问过的位置，需要使用一个与输入矩阵大小相同的辅助矩阵 visited，其中的每个元素表示该位置是否被访问过。当一个元素被访问时，将 visited 中的对应位置的元素设为已访问。

如何判断路径是否结束？由于矩阵中的每个元素都被访问一次，因此路径的长度即为矩阵中的元素数量，当路径的长度达到矩阵中的元素数量时即为完整路径，将该路径返回。

代码实现过程中，可以定义一个方向数组，来表示路径模拟的4个方向，如上图中4个红色的箭头所示。

//定义方向数组
 int[][] directions = {{0,1},{1,0},{0,-1},{-1,0}};

1. 从左上角顶点到右上角顶点，数组横坐标不变，纵坐标加1，因此，方向向量为 (0,1)
2. 从右上角顶点到右下角顶点，数组横坐标不变，纵坐标加1，因此，方向向量为 (1,0)
3. 从右下角顶点到左下角顶点，数组横坐标不变，纵坐标减1，因此，方向向量为 (0,-1)
4. 从左下角顶点到左上角顶点，数组横坐标减1，纵坐标不变，因此，方向向量为 (-1,0)

复杂度分析

• 时间复杂度：O(mn)，其中 m 和 n 分别是输入矩阵的行数和列数。矩阵中的每个元素都要被访问一次。
• 空间复杂度：O(mn)。需要创建一个大小为 m × n 的矩阵 visited 记录每个位置是否被访问过。

Solution

• java

class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        List<Integer> order = new ArrayList<Integer>();
        if(matrix == null || matrix.length == 0 || matrix[0].length == 0){
            return order;
        }
        int rows = matrix.length;
        int columns = matrix[0].length;
        //数组总元素
        int total = rows*columns;
        boolean[][] visited = new boolean[rows][columns];
        int row = 0;
        int column = 0;
        //定义方向数组
        int[][] directions = {{0,1},{1,0},{0,-1},{-1,0}};
        int directionIndex = 0;
        for(int i=0;i<total;i++){
            order.add(matrix[row][column]);
            visited[row][column] = true;  //标记已经访问
            int nextRow = row + directions[directionIndex][0];
            int nextColumn = column + directions[directionIndex][1];
            if(nextRow < 0 || nextRow >= rows || nextColumn < 0 || nextColumn >= columns || visited[nextRow][nextColumn]){
                directionIndex = (directionIndex+1)%4;
            }
            //更新directionIndex后，计算出新的row column
            row = row +  directions[directionIndex][0];
            column = column + directions[directionIndex][1];
        }
        return order;
    }
}

Approach 2-按层模拟

Analysis

可以将矩阵看成若干层，首先输出最外层的元素，其次输出次外层的元素，直到输出最内层的元素。

定义矩阵的第 k 层是到最近边界距离为 k 的所有顶点。例如，下图矩阵最外层元素都是第 1 层，次外层元素都是第 2 层，剩下的元素都是第 3 层。

[[1, 1, 1, 1, 1, 1, 1],
 [1, 2, 2, 2, 2, 2, 1],
 [1, 2, 3, 3, 3, 2, 1],
 [1, 2, 2, 2, 2, 2, 1],
 [1, 1, 1, 1, 1, 1, 1]]

对于每层，从左上方开始以顺时针的顺序遍历所有元素。假设当前层的左上角位于 (top,left)，右下角位于 (bottom,right)，按照如下顺序遍历当前层的元素。

1. 从左到右遍历上侧元素，依次为 (top,left) 到 (top,right)。
2. 从上到下遍历右侧元素，依次为 (top+1,right) 到 (bottom,right)。
3. 如果 left < right 且 top < bottom，则从右到左遍历下侧元素，依次为 (bottom,right−1) 到 (bottom,left+1)。以及从下到上遍历左侧元素，依次为 (bottom,left) 到 (top+1,left)。

遍历完当前层的元素之后，将 left 和 top 分别增加 1，将 right 和 bottom 分别减少 1，进入下一层继续遍历，直到遍历完所有元素为止。

复杂度分析

• 时间复杂度：O(mn)，其中 m 和 n 分别是输入矩阵的行数和列数。矩阵中的每个元素都要被访问一次。
• 空间复杂度：O(1)。除了输出数组以外，空间复杂度是常数。

Solution

• java

class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        List<Integer> order = new ArrayList<Integer>();
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
            return order;
        }
        int rows = matrix.length, columns = matrix[0].length;
        int left = 0, right = columns - 1, top = 0, bottom = rows - 1;
        while (left <= right && top <= bottom) {
            for (int column = left; column <= right; column++) {
                order.add(matrix[top][column]);
            }
            for (int row = top + 1; row <= bottom; row++) {
                order.add(matrix[row][right]);
            }
            if (left < right && top < bottom) {
                for (int column = right - 1; column > left; column--) {
                    order.add(matrix[bottom][column]);
                }
                for (int row = bottom; row > top; row--) {
                    order.add(matrix[row][left]);
                }
            }
            left++;
            right--;
            top++;
            bottom--;
        }
        return order;
    }
}

59. 螺旋矩阵 II

Description

• LeetCode-59. 螺旋矩阵 II

Approach 1-模拟

Analysis

参考 LeetCode Notes-54. 螺旋矩阵 中方法1的思路求解。

对于数组赋值，可以使用数组元素是否为0（数组初始化元素为0）来区分该元素是否已经被赋值。

复杂度分析

• 时间复杂度：O(n^2)，填充时候遍历了数组元素。
• 空间复杂度：O(n^2)，需要一个 n*n 的数组来存储结果。

Solution

• Java

class Solution {
    public int[][] generateMatrix(int n) {
        int[][] arr = new int[n][n];
        int[][] directions = {{0,1},{1,0},{0,-1},{-1,0}};
        int directionIndex = 0;
        int total = n*n;
        int row = 0;
        int col = 0;
        for(int i=1;i<=total;i++){
            arr[row][col] = i;
            int nextRow = row + directions[directionIndex][0];
            int nextCol = col + directions[directionIndex][1];
            //arr[row][col] != 0 标记元素已经被访问
            if(nextRow < 0 || nextRow >= n || nextCol <0 || nextCol >= n || arr[nextRow][nextCol] != 0){
                directionIndex = (directionIndex+1)%4;
            }
            //更新row col
            row = row + directions[directionIndex][0];
            col = col + directions[directionIndex][1];
        }
        return arr;
    }
}

14. 最长公共前缀

Description

• LeetCode-14. 最长公共前缀

Approach 1-横向扫描

Analysis

求解整个数组的最长公共前缀，可以

1. 先求解前2个元素的最长公共前缀 prefix
2. 再求解 prefix 和第3个元素的最长公共前缀，并更新 prefix
3. 再求解 prefix 和第4个元素的最长公共前缀，并更新 prefix
4. …

基于上述思路，对数组元素进行横向扫描，可以求解出整个数组的最长公共前缀。

复杂度分析

• 时间复杂度：O(mn)，其中 m 是字符串数组中的字符串的平均长度，n 是字符串的数量。最坏情况下，字符串数组中的每个字符串的每个字符都会被比较一次。
• 空间复杂度：O(1)。使用的额外空间复杂度为常数。

Solutiob

• java

class Solution {
    public String longestCommonPrefix(String[] strs) {
        if(strs == null || strs.length == 0) {
            return "";
        }
        String prefix = strs[0];
        int count = strs.length;
        for(int i=1;i<count;i++){
            prefix = longestCommonPrefix(prefix,strs[i]);
            if(prefix.length() == 0){
                //如果前缀字符串长度为0 可直接返回
                break;
            }
        }
        return prefix;
    }
    public String longestCommonPrefix(String str1,String str2){
        int count = Math.min(str1.length(),str2.length());
        int  index = 0;
        for(int i=0;i<count;i++){
            if(str1.charAt(i) != str2.charAt(i)){
                break;
            }
            index++;
        }
        return str1.substring(0,index);
    }

}

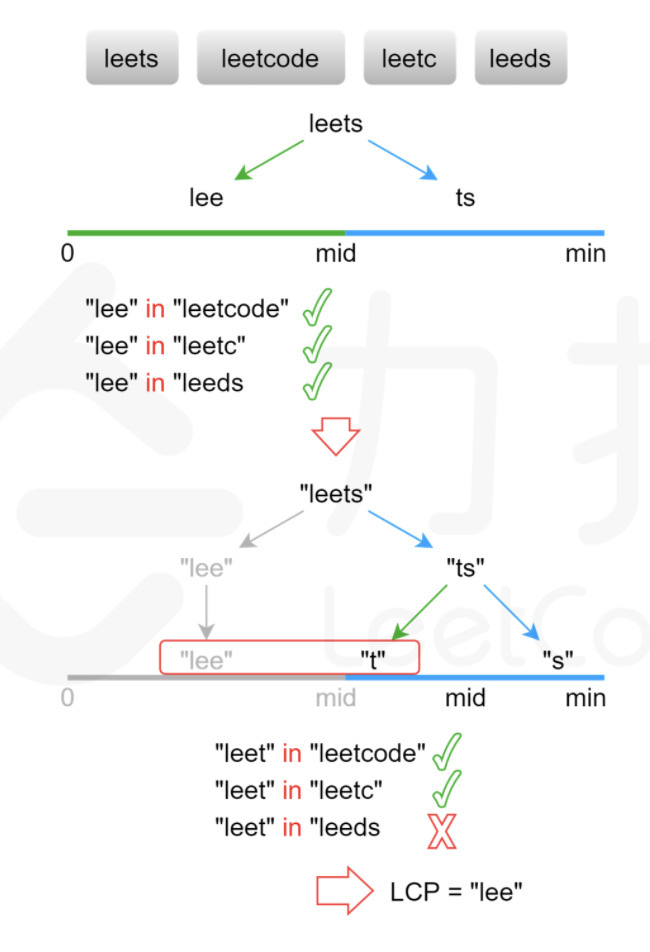
Approach 2-二分查找

Analysis

参见 leetcode-cn 官方题解。

显然，最长公共前缀的长度不会超过字符串数组中的最短字符串的长度。 用 minLength}minLength 表示字符串数组中的最短字符串的长度，则可以在 [0,minLength] 的范围内通过二分查找得到最长公共前缀的长度。每次取查找范围的中间值 mid，判断每个字符串的长度为 mid 的前缀是否相同，如果相同则最长公共前缀的长度一定大于或等于 mid，如果不相同则最长公共前缀的长度一定小于 mid，通过上述方式将查找范围缩小一半，直到得到最长公共前缀的长度。

复杂度分析

• 时间复杂度：$O(mn \log m)$，其中 m 是字符串数组中的字符串的最小长度，n 是字符串的数量。二分查找的迭代执行次数是 $O(\log m)$，每次迭代最多需要比较 mn 个字符，因此总时间复杂度是 $O(mn \log m)$。
• 空间复杂度：O(1)。使用的额外空间复杂度为常数。

Solution

• java

class Solution {
    public String longestCommonPrefix(String[] strs) {
        if(strs == null || strs.length == 0) {
            return "";
        }
        int minLength = Integer.MAX_VALUE;
        //计算数组中字符的最小长度
        for(String str:strs){
            minLength = Math.min(minLength,str.length());
        }
        int low = 0;
        int high =  minLength;
        //二分查找
        while(low < high){
            // int mid = (low+high)/2;
            int mid = (high - low + 1) / 2 + low;
            // int mid = low + (high - low) / 2;
            if(isCommonPrefix(strs,mid)){
                low = mid;
            }
            else{
                high = mid-1;
            }
        }
        return strs[0].substring(0,low);
    }
    public boolean isCommonPrefix(String[] strs, int length) {
        String str0 = strs[0].substring(0,length);
        int count = strs.length;
        for(int i=1;i<count;i++){
            String str = strs[i];
            for(int j=0;j<length;j++){
                if(str0.charAt(j) != str.charAt(j)){
                    return false;
                }
            }
        }
        return true;
    }
}

此处，对二分查找中 mid 的计算做如下说明

while(low < high>){
    // int mid = (low+high)/2;
    int mid = (high - low + 1) / 2 + low;
    // int mid = low + (high - low) / 2;
}

1. 不使用 mid = (low+high)/2，是因为数据相加容易产生溢出
2. 在数组长度大于1的情况下，一般使用 mid = low + (high - low) / 2 计算
3. 如果数组长度为1，这个时候 low=0, high=1，计算的 mid = low + (high - low) / 2 = 0，会造成无限循环。如果使用 mid = (high - low + 1) / 2 + low 计算，则 mid = 1 = high，在后续循环中执行 high = mid-1，从而使得 low = high，结束了 while 循环。

1300. 转变数组后最接近目标值的数组和

Description

• LeetCode-1300. 转变数组后最接近目标值的数组和

Approach 1-排序后遍历数组

Analysis

题意可以总结为，找到某个 value 值，将大于 value 的数组元素缩小到 value，使得数组总和最接近 target。

分析题意，有如下思路

1. 对数组进行排序。
2. 若数组本身求和小于等于 target，则没有必要再缩小某些值了，直接返回数组的最大值即可。
3. 否则，用 target 值除以数组长度，得到一个平均值，对平均值上下的两个整数值进行判断，并返回

于是乎，很容易有如下代码

//该代码并不能通过所有测试用例
class Solution {
    public int findBestValue(int[] arr, int target) {
        int max = 0;
        int value = 0;
        int minDistance = Integer.MAX_VALUE;
        int sum = 0;
        for(int num:arr){
            max = Math.max(max,num);
            sum += num;
        }
        if(sum <= target){
            return max;
        }
        //平均值  向下取整
        //后续对平均值向上取整也进行判断
        int avgValue = target/arr.length;
        if((target - avgValue*arr.length) < ((avgValue+1)*arr.length - target)){
            return avgValue;
        }
        else{
            return  avgValue+1;            
        }
        return 0;
    }
}

提交代码，会发现对于下述测试用例，计算结果并不符合预期

//测试用例
[1547,83230,57084,93444,70879]
71237


//预期正确结果
17422    

//程序返回的错误结果
14247

产生错误的原因是，若数组中有小于平均值的元素 arr[i]，在最后在和 target 值比较时，这些元素 arr[i] 并不会被替换为平均值参与计算，因此导致了这种情况下，计算出的数组平均值并不是符合要求的 value 值。

下面对求解思路进行逻辑完善。

1. 对数组进行排序。
2. 若数组本身求和小于等于 target，则没有必要再缩小某些值了，直接返回数组的最大值即可。
3. 否则，用 target 值除以数组长度，得到一个平均值 avgValue。
4. 若计算出的平均值 avgValue，小于数组的每一个元素，则说明数组的每一个元素值都会被替换。此时结果一定是平均值上下的两个整数中的一个。
5. 若不满足步骤4，则对数组进行遍历

• 对于已经排序好的数组，分别取 value 为数组中的第 i 个元素值，直到发现 sum >= target。
• 此时记录第 i 个元素左边的元素和为 sumLeft，那么如果 i 和 i 右边的数字全部变成 ans = (target - sumLeft)/(n - i)，这个时候总和就是 sumLeft + ans*(n - i) = target。
• 这个时候计算出的 ans 就是最后要返回的结果，对其上下两个临近的整数值判断并返回正确结果即可。

复杂度分析

• 时间复杂度：O((N)，进行了数组遍历
• 空间复杂度：O(1)。

在 leetcode-cn 平台测试，方法1执行用时4ms，内存消耗40MB；下述方法2执行用时32ms，内存消耗40.1MB；

Solution

• java

class Solution {
    public int findBestValue(int[] arr, int target) {
        Arrays.sort(arr);   //排序
        int sumArr = 0;
        int arrLength =  arr.length;
        for(int num:arr){
            sumArr += num;
        }
        if(sumArr <= target){ //若数组和不大于target，返回数组的最大值
            return arr[arrLength-1];
        }
        //全部替换为数组最小值，求和若大于target
        if(arr[0]*arrLength >= target){
            int avgValue = target/arrLength;
            if((target - avgValue*arrLength) < ((avgValue+1)*arrLength - target)){
                return avgValue;
            }
            else{
                return  avgValue+1;
            }
        }

        int sumLeft = arr[0];
        for(int i=1;i<arrLength;i++){
            int sum = sumLeft + arr[i]*(arrLength-i);
            //最开始时，sum是小于target的
            //从sum<target  到 sum>=target，说明中间一定遇到了最合适的value值                                                                                   
            if(sum >= target){
                int ans = (target - sumLeft)/(arrLength - i);
                if(target - sumLeft - ans*(arrLength - i) <= (ans + 1) * (arrLength - i) + sumLeft - target){
                    return ans;    
                }
                else{
                    return ans + 1;
                }
            }
            sumLeft += arr[i];
        }

        return 0;
    }
}

Approach 2-枚举+二分查找

Analysis

分析题意可知，要返回的 value 值的取值范围在区间 [1,arrMaxNum]中，即最小值可能是1，最大值是数组元素的最大值。因此可以枚举 value 的可能取值进行求解。

当枚举到 value=x 时，我们需要将数组 arr 中所有小于等于 x 的值保持不变，所有大于 x 的值变为 x。要实现这个操作，我们可以将数组 arr 先进行排序，随后进行二分查找，找出数组 arr 中最小的比 x 大的元素 arr[i]。此时数组的和变为

arr[0] + ... + arr[i - 1] + x * (n - i)

为了加速求和操作，我们可以预处理出数组 arr 的前缀和，这样数组求和的时间复杂度即能降为 O(1)。我们将和与 target 进行比较，同时更新答案即可。

复杂度分析

• 时间复杂度：$O((N + C)\log N)$，其中 N 是数组 arr 的长度，C 是一个常数，为数组 arr 中的最大值，不会超过 $10^5$。排序需要的时间复杂度为 $O(N\log N)$，二分查找的单次时间复杂度为 $O(\log N)$，需要进行 C 次。
• 空间复杂度：O(N)。我们需要 O(N) 的空间用来存储数组 arr 的前缀和，排序需要 O(logN) 的栈空间，因此最后总空间复杂度为 O(N)。

Solution

• java

class Solution {
    public int findBestValue(int[] arr, int target) {
        Arrays.sort(arr);
        int n = arr.length;
        //数组前缀和 prefix[i]表示数组前i个元素的和  
        // prefix[1] = arr[0]   prefix[0] = 0  
        int[] prefix =  new int[n+1];
        for(int i=1;i<n+1;i++){
            prefix[i] = arr[i-1] + prefix[i-1];
        }

        int ans = 0;
        int diff = target;
        for(int i=1;i<=arr[n-1];i++){
            int index = Arrays.binarySearch(arr,i);
            if(index < 0){
                //未找到 计算出正确的插入点
                // index = -(insert point + 1)
                // index = -index-1 = (insert point + 1)-1 = insert point
                index = -index-1;
            }
            int cur = prefix[index] + (n-index)*i;
            if(Math.abs(cur - target) < diff){
                ans = i;
                diff = Math.abs(cur - target);
            }
        }
        return ans;



    }
}