Do one thing at a time and do well

0%

LeetCode题解-007

发表于 更新于 分类于 阅读次数： Disqus：
  • 记录LeetCode题目笔记，汇总LeetCode解答记录

Changelog

  • 2020/05/12，撰写
  • 2020/05/18，添加 滚动数组 方法介绍
  • 2020/05/19，整理完成

Overview

560. 和为K的子数组

Description

Approach 1-枚举

参考 leetcode-cn 官方题解。

Analysis

考虑以 i 结尾和为 k 的连续子数组个数，我们需要统计符合条件的下标 j 的个数，其中 0 ≤ j ≤i 且 [j..i] 这个子数组的和恰好为 k。

我们可以枚举 [0..i] 里所有的下标 j 来判断是否符合条件，可能有读者会认为假定我们确定了子数组的开头和结尾，还需要 O(n) 的时间复杂度遍历子数组来求和，那样复杂度就将达到 O(n^3)，从而无法通过所有测试用例。

但是如果我们知道 [j,i] 子数组的和，就能 O(1) 推出 [j-1,i] 的和，因此这部分的遍历求和是不需要的，我们在枚举下标 j 的时候已经能 O(1) 求出 [j,i] 的子数组之和。

复杂度分析

  • 时间复杂度：O(n^2)，其中 n 为数组的长度。枚举子数组开头和结尾需要 O(n^2) 的时间，其中求和需要 O(1) 的时间复杂度，因此总时间复杂度为 O(n^2)
  • 空间复杂度：O(1)，只需要常数空间存放若干变量。

Solution

  • Java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public int subarraySum(int[] nums, int k) {
        int count = 0;
        int sum = 0;
        for(int i=0;i<nums.length;i++){
            sum = 0;
            for(int j=i;j>=0;j--){
                sum += nums[j];
                if(sum == k){
                    count++;
                }
            }
        }
        return count;
    }
}

例如，针对数组 {3,4,7,2,-3,1,4,2}，k=7的情况，共有4个子数组满足条件

  1. {3,4}
  2. {7}
  3. {7,2,-3,1}
  4. {1,4,2}

Approach 2-前缀和+哈希表

参考 leetcode-cn 官方题解。

Analysis

方法一的瓶颈在于对每个 i，我们需要枚举所有的 j 来判断是否符合条件，这一步是否可以优化呢？答案是可以的。

我们定义 pre[i] 为 [0..i] 里所有数的和，则 pre[i] 可以由 pre[i-1] 递推而来

1
pre[i]=pre[i−1]+nums[i]

那么 [j..i] 这个子数组和为 k 这个条件，我们可以转化为

1
pre[i] − pre[j−1] == k

简单移项可得符合条件的下标 j 需要满足

1
pre[j−1]==pre[i]−k

所以我们考虑以 i 结尾的和为 k 的连续子数组个数时，只要统计有多少个前缀和为 pre[i]−k 的 pre[j] 即可。

我们建立哈希表 mp，以和为键，出现次数为对应的值，记录 pre[i] 出现的次数，从左往右边更新 mp 并计算答案，那么以 i 结尾的答案 mp[pre[i]-k] 即可在 O(1) 时间内得到。最后的答案即为所有下标结尾的和为 k 的子数组个数之和。

需要注意的是，从左往右边更新边计算的时候已经保证了 mp[pre[i]-k] 里记录的 pre[j] 的下标范围是 0 ≤ j ≤i。同时，由于 pre[i] 的计算只与前一项的答案有关，因此我们可以不用建立 pre 数组，直接用 pre 变量来记录 pre[i-1] 的值即可。

参考 leetcode-cn 官方题解的辅助演示动画，加深理解。下面针对数组 {3,4,7,2,-3,1,4,2}，k=7的情况，进行逐步分析

  1. mp 初始化时，需要插入 (0,1)，一方面是表示前缀和为0的情况出现了1次（即空数组），另一方面也是为了后续统计 pre[i]−k 等于 0 的情况，如下图所示

  1. i=0时，pre 为 3，因此在 map 插入 (3,1)

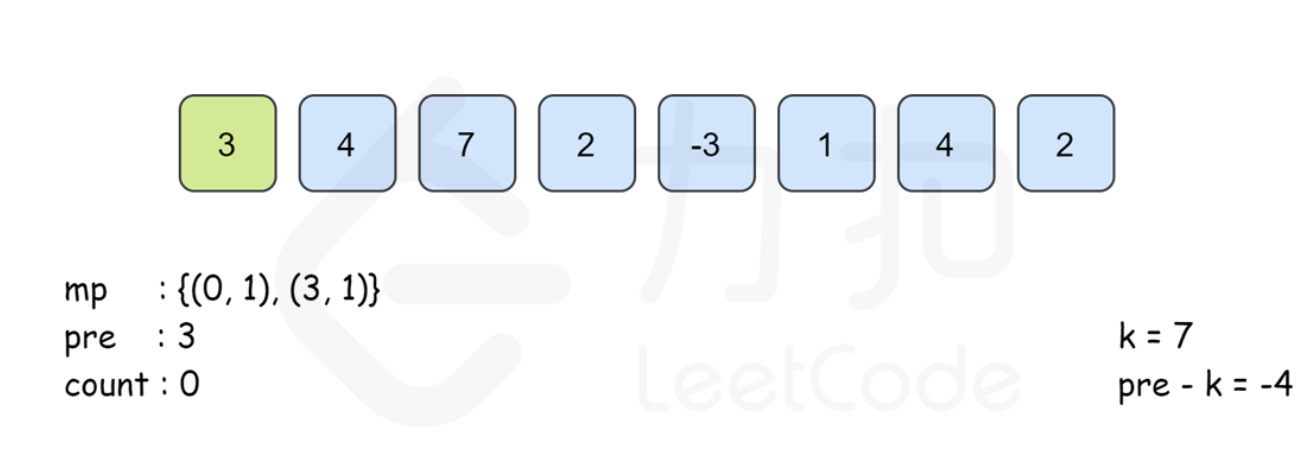
  1. i=1时，pre 为 7，因此在 map 插入 (7,1)。此时 pre-k = 0，在 map 中已经存在 key=0的 value 值。因此，执行 count += mp.get(pre - k); 后，计数值 count 等于1，表示区间 [0,1] 的子数组 {3,4} 满足和等于 7 的条件

  1. i=2时，pre 为 14，因此在 map 插入 (14,1)。此时 pre-k = 7，在 map 中已经存在 key=7的 value 值。因此，执行 count += mp.get(pre - k); 后，计数值 count 等于2，表示区间 [2,2] 的子数组 {7} 满足和等于 7 的条件

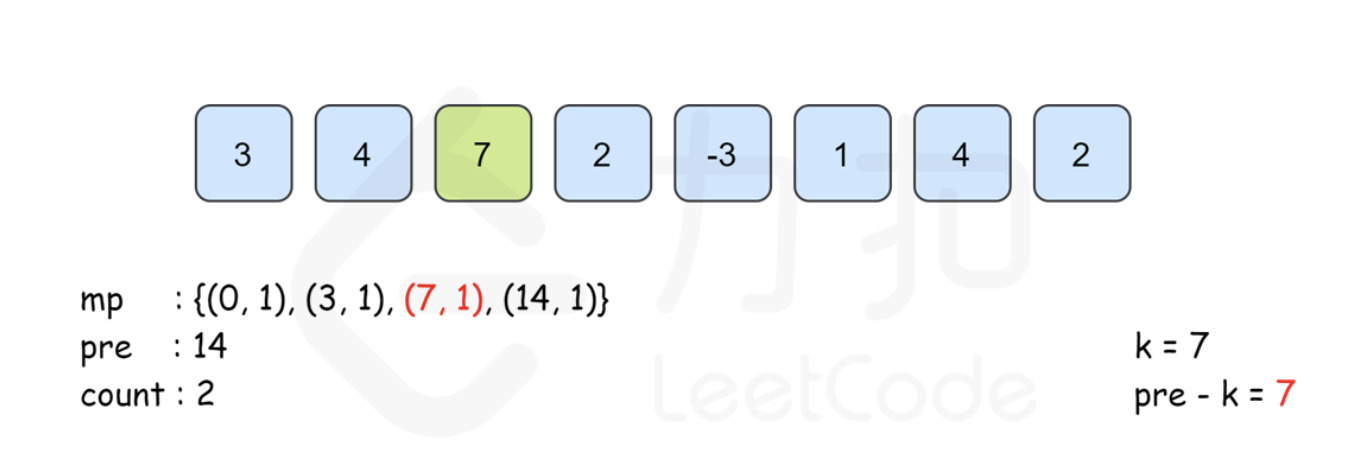
  1. i=3时，pre 为 16，因此在 map 插入 (16,1)。此时 pre-k = 9，在 map 中找不到 key=9的 value 值。

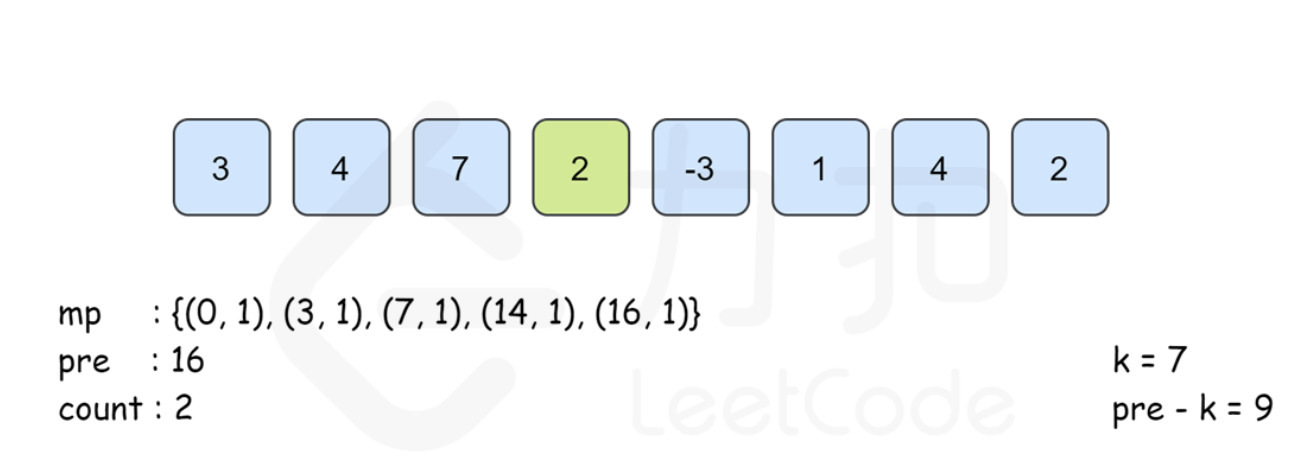
  1. i=4时，pre 为 13，因此在 map 插入 (13,1)。此时 pre-k = 6，在 map 中找不到经存在 key=6的 value 值。

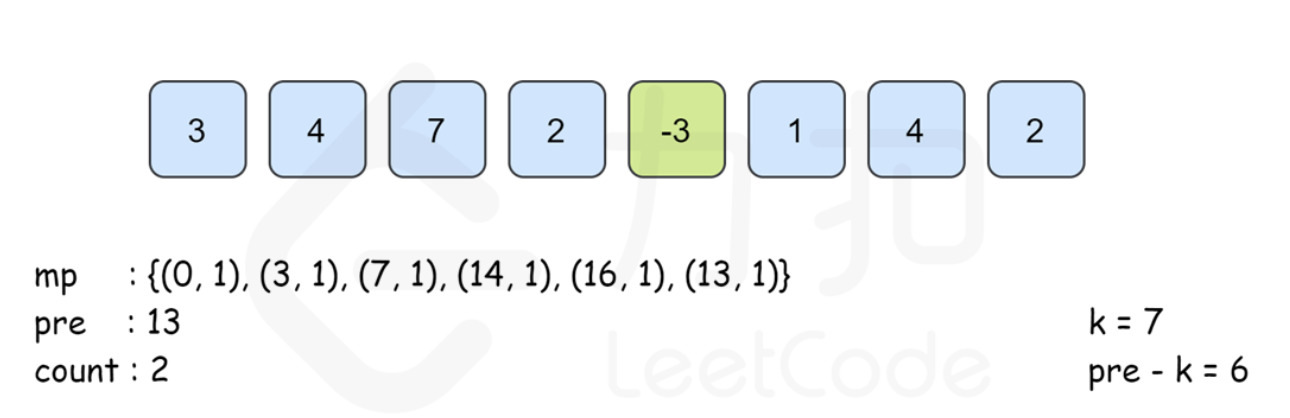
  1. i=5时，pre 为 14，此时 map 中已经存在 key=14 的值，因此 map 中更新为 (14,2)。此时 pre-k = 7，在 map 中已经存在 key=7的 value 值。因此，执行 count += mp.get(pre - k); 后，计数值 count 等于3，表示区间 [2,5] 的子数组 {7,2-3,1} 满足和等于 7 的条件

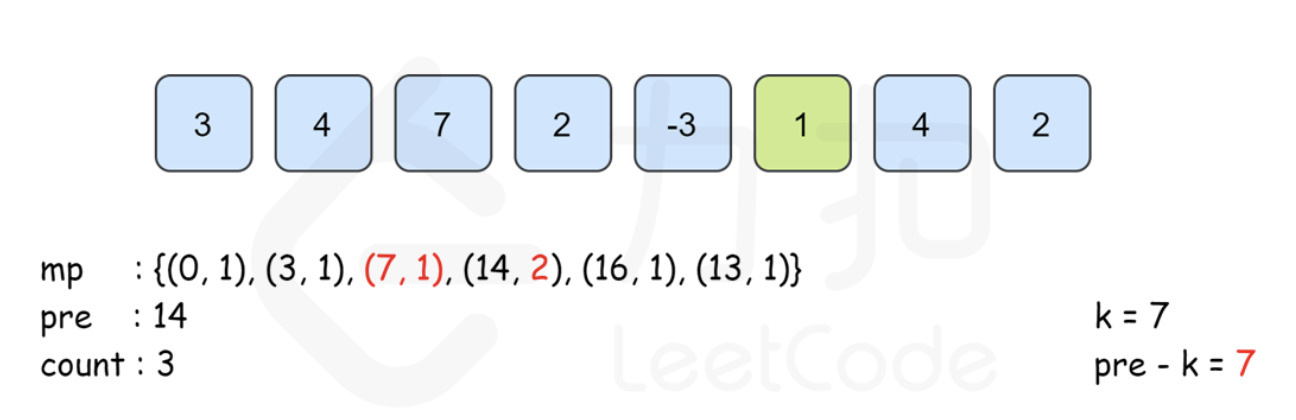
  1. i=6时，pre 为 18，因此在 map 插入 (18,1)。此时 pre-k = 11，在 map 中找不到 key=11的 value 值。

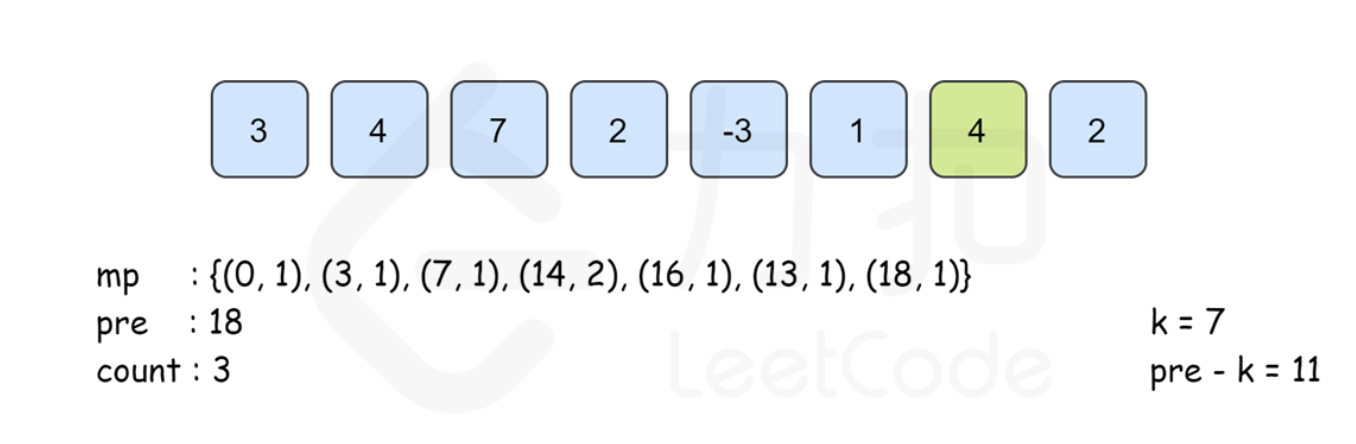
  1. i=7时，pre 为 20，因此在 map 插入 (20,1)。此时 pre-k = 13，在 map 中已经存在 key=13的 value 值。因此，执行 count += mp.get(pre - k); 后，计数值 count 等于4，表示区间 [5,7] 的子数组 {1,4,2} 满足和等于 7 的条件

复杂度分析

  • 时间复杂度：O(n)，其中 n 为数组的长度。我们遍历数组的时间复杂度为 O(n)，中间利用哈希表查询删除的复杂度均为 O(1)，因此总时间复杂度为 O(n)
  • 空间复杂度：O(n)，其中 n 为数组的长度。哈希表在最坏情况下可能有 n 个不同的键值，因此需要 O(n) 的空间复杂度。

Solution

  • Java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

class Solution {
    public int subarraySum(int[] nums, int k) {
        int count = 0, pre = 0;
        HashMap < Integer, Integer > mp = new HashMap < > ();
        //前缀和为0的情况，即空数组
        mp.put(0, 1);
        for (int i = 0; i < nums.length; i++) {
            pre += nums[i];
            if (mp.containsKey(pre - k)){
                 //统计次数
                 count += mp.get(pre - k);
            }
            //记录pre出现的次数
            mp.put(pre, mp.getOrDefault(pre, 0) + 1);
        }
        return count;
    }
}

25. K 个一组翻转链表

Description

Approach 1-常规求解

Analysis

常规思路求解，遍历链表，若移动了K个节点，则对这个区间的链表进行翻转，翻转链表的过程并不难，过程可以参考 LeetCode-206. Reverse Linked List（反转链表） 。

本题目的难点是在翻转链表后，需要将翻转后的子链表的头部和上一个子链表连接，同时将翻转后的子链表的尾部和下一个子链表连接，如下图所示。

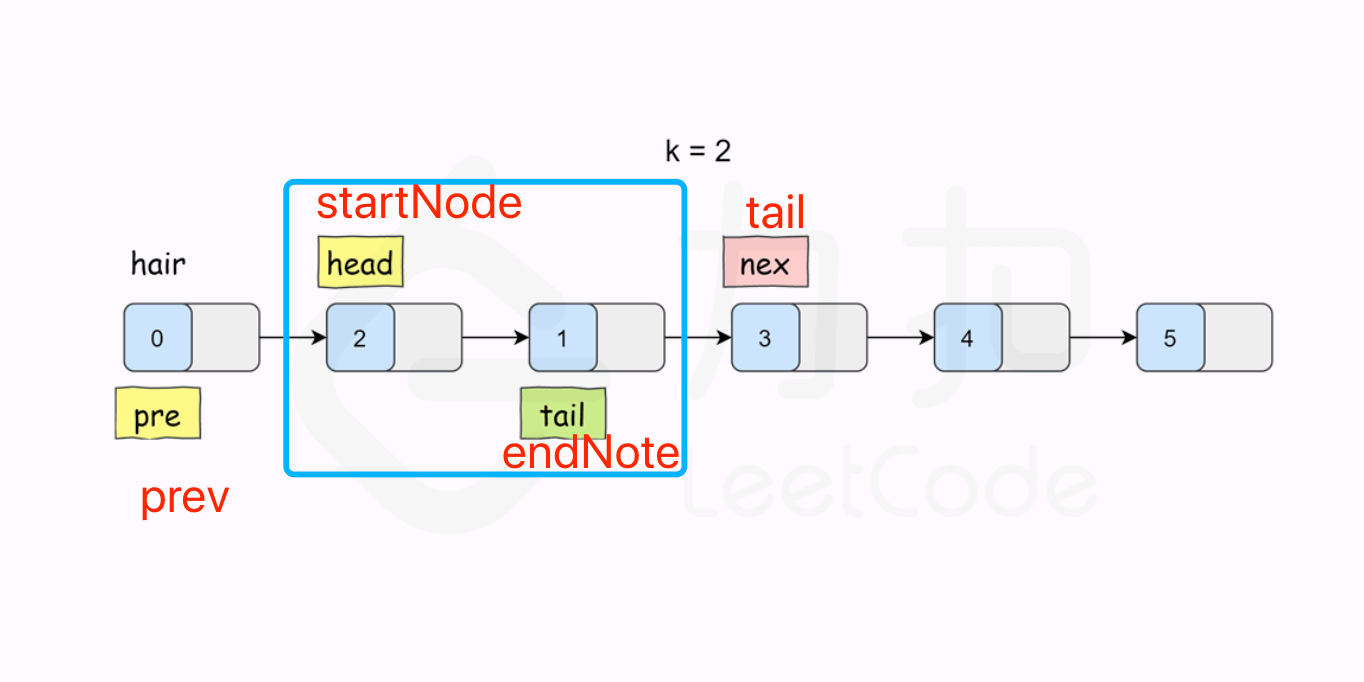
为了方便表示，引入 prev 和 tail 分别表示翻转链表的上一个节点和下一个节点，使用 startNode 和 endNode 分别表示翻转链表的首尾节点。

这里需要注意的是，对于链表的前 K 个长度的子链表，这个时候 prev 是不存在的。为了后续处理方便，可以在链表头部插入一个辅助节点 hair，如上图所示。

下面分析下如何返回最后的链表结果。在程序过程中

  • 若没有发生链表翻转，则返回 hair.next 即可。
  • 若发生了链表翻转，则记录第一次链表翻转的情况，并将 hair.next 指向翻转后的链表头部，最后程序结束是，同样返回 hair.next。

具体细节，可以参考 leetcode-cn 官网题解的动画分析。

算法复杂度分析如下

  • 时间复杂度：O(n)，其中 n 为链表的长度。head 指针会在 O(floor(n/k)) 个结点上停留，每次停留需要进行一次 O(k) 的翻转操作。
  • 空间复杂度：O(1)，我们只需要建立常数个变量。

Solution

  • Java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public ListNode reverseKGroup(ListNode head, int k) {
        if(head == null || head.next == null || k == 0 || k == 1) {
            return head;
        }
        ListNode hair = new ListNode(0);
        hair.next = head;
        ListNode prev = hair;
        ListNode tail = hair;
        ListNode startNode = head;
        ListNode endNode = head;
        int reverseLength = 1;
        boolean hasReverse = false;
        while(head != null && head.next != null){
            head = head.next;
            reverseLength ++;
            if(reverseLength == k){
                endNode = head;
                tail = endNode.next;
                startNode = prev.next;
                reverseList(startNode,k);
                if(!hasReverse){
                    hair.next = endNode; 
                    hasReverse = true;
                }
                prev.next = endNode;
                startNode.next = tail;
                prev = startNode;
                tail = startNode;

                reverseLength =1;
                head = tail.next;
            }
        }
        return hair.next;
    }

    public void reverseList(ListNode head,int length){
        ListNode prev = null;
        ListNode curr = head;
        while(length >0){
            length--;
            ListNode nextTemp = curr.next;
            curr.next = prev;
            prev = curr;
            curr = nextTemp;
        }
    }
}

53. 最大子序和

Description

Approach 1-动态规划

Analysis

参考 leetcode-cn 官方题解。

假设 nums 数组的长度是 n，下标从 0 到 n-1。

我们用 $a_i$ 代表 nums[i]，用 f(i) 代表以第 i 个数结尾的 「连续子数组的最大和」，那么很显然我们要求的答案就是

1
\max_{0 \leq i \leq n - 1} \{ f(i) \}

因此我们只需要求出每个位置的 f(i)，然后返回 f 数组中的最大值即可。

那么我们如何求 f(i) 呢？不难列出如下动态转移方程

1
f(i) = \max \{ f(i - 1) + a_i, a_i \}

算法复杂度分析

  1. 时间复杂度：O(n)
  2. 空间复杂度：O(n)，创建了一个长度为 n 的 f 数组

Solution

  • Java
1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
    public int maxSubArray(int[] nums) {
        int res = nums[0];
        int[] pre = new int[nums.length];
        pre[0] = nums[0];
        for(int i=1;i<nums.length;i++){
            pre[i] = Math.max(pre[i-1]+nums[i],nums[i]);
            res = Math.max(pre[i],res);
        }
        return res;
    }
}

Approach 2-动态规划+滚动数组优化空间

Analysis

在 Approach 1 的基础上继续分析，使用滚动数组的思想对空间复杂度进行优化。

1
f(i) = \max \{ f(i - 1) + a_i, a_i \}

在动态转移方程中，考虑到 f(i) 只和 f(i-1) 相关，于是我们可以只用一个变量 pre 来维护对于当前 f(i) 的 f(i-1) 的值是多少，从而让空间复杂度降低到 O(1)，这有点类似 「滚动数组」 的思想。

算法复杂度分析

  1. 时间复杂度：O(n)
  2. 空间复杂度：O(1)

Solution

  • Java
1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
    public int maxSubArray(int[] nums) {
        int res = nums[0];
        int pre = 0;
        for(int i=0;i<nums.length;i++){
            pre = Math.max(pre+nums[i],nums[i]);
            res = Math.max(pre,res);
        }
        return res;

    }
}

滚动数组

ref

思想介绍

滚动数组 是动态规划中的一种编程思想。简单的理解就是让数组滚动起来，每次都使用固定的几个存储空间，来达到压缩，节省存储空间的作用。

因为动态规划是一个自底向上的扩展过程，我们常常需要用到的是连续的解，前面的解往往可以舍去。所以用滚动数组优化是很有效的。利用滚动数组的话在 N 很大的情况下可以达到压缩存储的作用。

Demo1-斐波那契数列

此处以求解斐波那契数列为例进行说明。如下代码示例，求解斐波那契数列的第 80 项。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#include<stdio.h>
int main()
{
    int i;
    long long d[80];
    d[0]=1;
    d[1]=1;
    for(i=2;i<80;i++)
    {
        d[i]=d[i-1]+d[i-2];
    }
    printf("%lld\n",d[79]);
    return 0;
}

上述代码中，创建了一个长度为 N=80 的数组。如果 N 的值很大，则会占用很大的存储空间。

查看状态转移方程 d[i]=d[i-1]+d[i-2]，可以发现，待求解的 d[i]，只和其前面两项 d[i-1] 和 d[i-2] 有关，和其余项无关。

因此，可以只创建一个长度为 3 的数组，将数组“滚动”起来，将待求解的项存储在 d[2] 中，其依赖的前两项存储在 d[1] 和 d[0] 中。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#include<stdio.h>
int main()
{
    int i;
    long long d[3];
    d[1]=1;
    d[2]=1;
    for(i=2;i<80;i++)
    {
        d[0]=d[1];
        d[1]=d[2];
        d[2]=d[0]+d[1]; 
    }
    printf("%lld\n",d[2]);
    return 0;
}

Demo2-leetcode-子序问题

  • leetcode-53. 最大子序和
  • leetcode-152. 乘积最大子数组

参考上述两道题目中的 Approach 2-动态规划+滚动数组优化空间。

152. 乘积最大子数组

Description

Approach 1-动态规划

Analysis

参考 leetcode-cn 官方题解。

如果我们用 $f_{\max}(i)$ 表示以第 i 个元素结尾的乘积最大子数组的乘积，a 表示输入参数 nums，那么根据 leetcode-53. 最大子序和 的经验，我们很容易推导出这样的状态转移方程

1
f_{\max}(i) = \max_{i = 1}^{n} \{ f(i - 1) \times a_i, a_i \}

它表示以第 i 个元素结尾的乘积最大子数组的乘积，可以考虑 $a_i$ 加入前面的 $f_{\max}(i - 1)$ 对应的一段，或者单独成为一段，这里两种情况下取最大值。

求出所有的 $f_{\max}(i)$ 之后选取最大的一个作为答案。

可是在这里，这样做是错误的。为什么呢？

因为这里的定义并不满足 「最优子结构」。具体地讲，如果 $a = \{ 5, 6, -3, 4, -3 \}$，那么此时 $f_{\max}$ 对应的序列是 $\{ 5, 30, -3, 4, -3 \}$。按照前面的算法我们可以得到答案为 30，即前两个数的乘积，而实际上答案应该是全体数字的乘积。我们来想一想问题出在哪里呢？问题出在最后一个 -3 所对应的 $f_{\max}$ 的值既不是 -3，也不是 4 × −3，而是 $5 \times 30 \times (-3) \times 4 \times$。

所以我们得到了一个结论：当前位置的最优解未必是由前一个位置的最优解转移得到的。

我们可以根据正负性进行分类讨论。

  1. 考虑当前位置如果是一个负数的话，那么我们希望以它前一个位置结尾的某个段的积也是个负数，这样就可以负负得正，并且我们希望这个积尽可能 「负得更多」，即尽可能小。
  2. 如果当前位置是一个正数的话，我们更希望以它前一个位置结尾的某个段的积也是个正数，并且希望它尽可能地大。
  3. 于是这里我们可以再维护一个 $f_{\min}(i)$，它表示以第 i 个元素结尾的乘积最小子数组的乘积，那么我们可以得到这样的动态规划转移方程
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
\begin{aligned} 
f_{\max}(i) &= \max_{i = 1}^{n} \{ f_{\max}(i - 1) \times a_i, f_{\min}(i - 1) \times a_i, a_i \} \\ f_{\min}(i) &= \min_{i = 1}^{n} \{ f_{\max}(i - 1) \times a_i, f_{\min}(i - 1) \times a_i, a_i \} 
\end{aligned}
```	
 

它代表第 `i` 个元素结尾的乘积最大子数组的乘积 `$f_{\max}(i)$`，可以考虑把 `$a_i$` 加入第 `i - 1` 个元素结尾的乘积最大或最小的子数组的乘积中，二者加上 `$a_i$`，三者取大，就是第 `i` 个元素结尾的乘积最大子数组的乘积。

第 `i` 个元素结尾的乘积最小子数组的乘积 `$f_{\min}(i)$` 同理。


算法复杂度分析
1. 时间复杂度： `O(n)`，遍历了数组
2. 空间复杂度： `O(n)`，引入了空间为 `n` 的辅助数组

#### Solution

* Java

```java
class Solution {
    public int maxProduct(int[] nums) {
        if(nums.length == 1) return nums[0];
        int max = nums[0];
        int[] imax = new int[nums.length];
        int[] imin = new int[nums.length];
        imax[0] = nums[0];
        imin[0]  = nums[0];
        for(int i=1;i<nums.length;i++){
            //保存临时变量
            int tmpMax = imax[i-1];
            int tmpMin = imin[i-1];
            imax[i] = Math.max(tmpMax*nums[i],tmpMin*nums[i]);
            imax[i] = Math.max(imax[i],nums[i]);
            imin[i] = Math.min(tmpMax*nums[i],tmpMin*nums[i]);
            imin[i] = Math.min(imin[i],nums[i]);
        }
        for(int i=0;i<nums.length;i++){
            max = Math.max(max,imax[i]);
        }
        return max;
    }
}

Approach 2-动态规划+滚动数组优化空间

Analysis

在 Approach 1 的基础上进一步对空间复杂度进行优化。

由于第 i 个状态只和第 i-1 个状态相关，根据 「滚动数组」 思想，我们可以只用两个变量来维护 i−1 时刻的状态，一个维护 $f_{\max}$，一个维护 $f_{\min}$。细节参见代码。

算法复杂度分析

  1. 时间复杂度：O(n)
  2. 空间复杂度：优化后只使用常数个临时变量作为辅助空间，与 n 无关，故渐进空间复杂度为 O(1)

Solution

  • Java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public int maxProduct(int[] nums) {
        if(nums.length == 1) return nums[0];
        int max = nums[0];
        int imax = nums[0];
        int imin = nums[0];
        for(int i=1;i<nums.length;i++){
            //保存临时变量
            int tmpMax = imax;
            int tmpMin = imin;
            imax = Math.max(tmpMax*nums[i],tmpMin*nums[i]);
            imax = Math.max(imax,nums[i]);
            imin = Math.min(tmpMax*nums[i],tmpMin*nums[i]);
            imin = Math.min(imin,nums[i]);
            max = Math.max(imax,max);
        }
        return max;
    }
}

680. 验证回文字符串 II

Description

Approach 1-贪心算法+双指针

Analysis

参考 leetcode-cn 官方题解。 此处仅给出必要的分析。

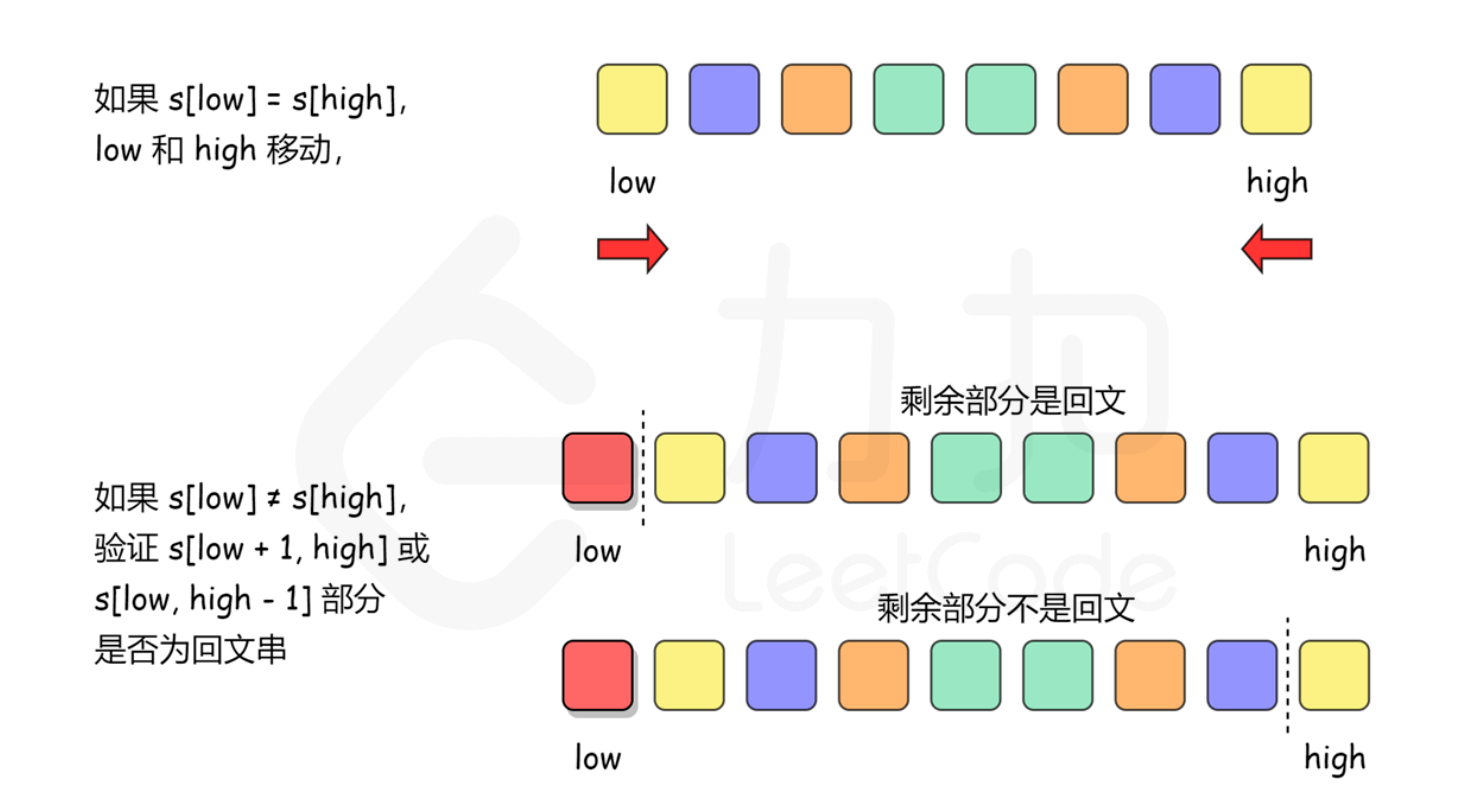
如上图所示，使用贪心算法+双指针求解。

  1. 如果不考虑 可以最多删除一个字符 的条件，对字符串是否回文进行判断 —— 使用两个指针分别指向字符串的头部和尾部，若指针指向的字符相等，则指针向中间靠拢，继续循环判断。
  2. 现在考虑下 可以最多删除一个字符 的条件 —— 若 s[low] != s[high]，下面需要分两种情况考虑
    • 删除 s[low] 字符，考虑 [low+1,high] 子区间
    • 删除 s[high] 字符，考虑 [low,high-1] 子区间
    • 上述两个子区间只要有一个满足回文串条件，则可以认为整个字符串是回文串

复杂度分析

  1. 时间复杂度：O(n)，其中 n 是字符串的长度。判断整个字符串是否是回文字符串的时间复杂度是 O(n)；遇到不同字符时，判断两个子串是否是回文字符串的时间复杂度也都是 O(n)。
  2. 空间复杂度：O(1)，只需要维护有限的常量空间。

Solution

  • Java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class Solution {
    public boolean validPalindrome(String s) {
        if(s.length() == 0 || s.length() == 1) return true;
        boolean flag = true;
        int length = s.length();
        int low = 0;
        int high = length-1;
        while(low<high){
            char start = s.charAt(low);
            char end = s.charAt(high);
            if(start == end){
                low++;
                high--;
            } else{
                boolean flag1 = true;
                boolean flag2 = true;
                //去除start字符
                for(int i=low+1,j=high;i<j;i++,j--){
                    char start1 = s.charAt(i);
                    char end1 = s.charAt(j);
                    if(start1 != end1){
                        flag1 = false;
                        break;
                    }
                }
                //去除end字符
                for(int i=low,j=high-1;i<j;i++,j--){
                    char start2 = s.charAt(i);
                    char end2 = s.charAt(j);
                    if(start2 != end2){
                        flag2 = false;
                        break;
                    }
                }
                 //此处直接返回，不需要再进行后续的while循环了
                 //不然会代码超时
                return (flag1 || flag2); 
                // flag = flag1 || flag2;
            }
        }
        return true;

    }
}

这里需要说明的是，在执行下述代码时，

  • 需要直接返回 return (flag1 || flag2);，不需要再进行后续的 while 循环了。这样可以保证时间复杂度是 O(n)。
  • 若使用 flag = flag1 || flag2; ，则时间复杂度会是 O(n^2)，代码会执行超时。
1
2
3
4
//此处直接返回，不需要再进行后续的while循环了
//不然会代码超时
return (flag1 || flag2); 
// flag = flag1 || flag2;