Do one thing at a time and do well

0%

LeetCode题解-003

发表于 分类于 阅读次数： Disqus：
  • 记录LeetCode题目笔记，汇总LeetCode解答记录

Overview

191. Number of 1 Bits（位1的个数）

Description

本问题中，计数了一个无符号整数的位，结果称为 pop count，或 汉明权重。

Approach 1：除K取余法

Analysis

  • 除K取余法，利用 num%2 和 num/2 不断取出数字的二进制数值。
  • 需要注意的是，在如Java语言中，不能使用 while(num>0) 进行判断。因为Java编译器使用二进制补码记法来表示有符号整数。例如输入 11111111111111111111111111111101， 会被作为 -3 处理。
  • 因此，在Java中应该避免取模和除法操作，使用 (num&1) == 1 代替 num%2；使用无符号右移 num >>> 1 代替 num/2。
  • 在C++中，若使用无符号类型 uint32_t 作为输入类型，可以直接使用 while(num>0) 作为循环判断。

Java 中，>>> 为无符号右移，>> 为有符号右移。

  • 时间复杂度：O(1)。运行时间依赖于数字 n 的位数。本题中是一个32位数字，因此时间复杂度位为 O(1)。
  • 空间复杂度：O(1)，没有使用额外的空间。

Solution

  • C++
1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    int hammingWeight(uint32_t n) {
        int total = 0;
        while(n>0){ //输入类型为无符号类型，因此可以直接使用n>0进行判断
            total += n%2;
            n /=2;
            //  n = n >>1; //也可使用移位操作
        }
        return total;
    }
};
  • Java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
public class Solution {
    // you need to treat n as an unsigned value
    public int hammingWeight(int n) {
        int total = 0;
        while(n != 0){
            if((n&1) == 1){
                total++; //不要使用取模操作
            }
            n = n >>> 1; //会有负数情况，因此应该使用无符号右移
            //Java 中，`>>>` 为无符号右移，`>>` 为有符号右移。
        }
        return total;
    }
}

或者采用如下实现

1
2
3
4
5
6
7
8
9
10
11
public int hammingWeight(int n) {
    int bits = 0;
    int mask = 1;
    for (int i = 0; i < 32; i++) { //最大32位
        if ((n & mask) != 0) {
            bits++;
        }
        mask <<= 1;
    }
    return bits;
}

Approach 2：位操作小技巧 - n&(n-1)

Analysis

对前面的算法进行优化。

不再检查数字的每一个位，而是不断把数字最后一个 1 反转，并把计数加1。当数字变成 0 的时候偶，我们就知道它没有 1 的位了，此时返回计数。

这里关键的想法是对于任意数字 n ，将 n 和 n - 1 做与运算，不断循环，最后一定会把 1 的位变成 0。

为什么？考虑 n 和 n - 1 的二进制表示。

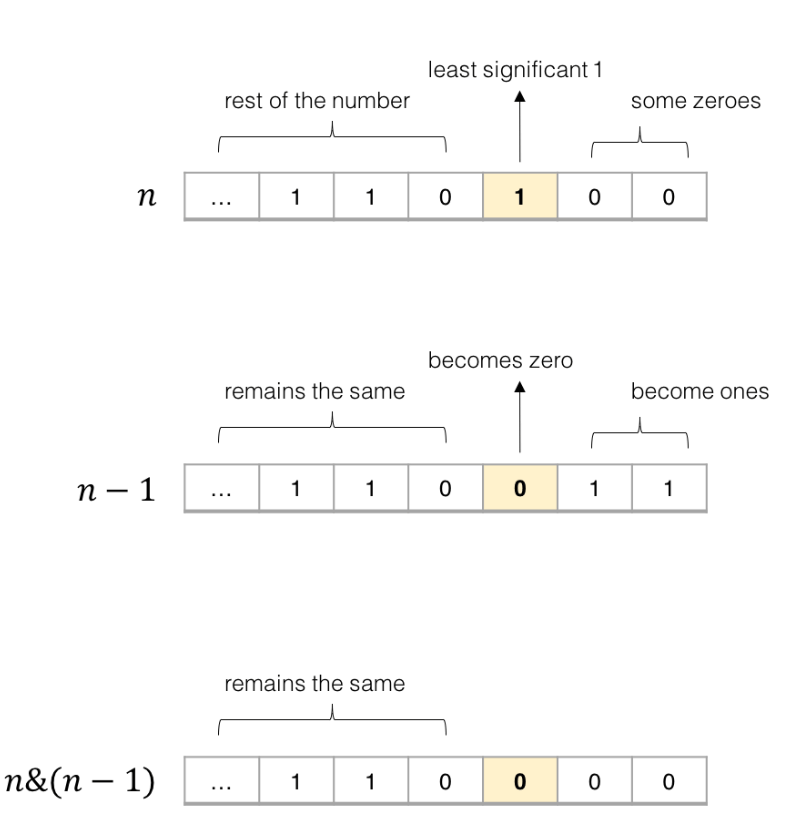
在二进制表示中，数字 n 中最低位的 1 总是对应 n - 1 中的 0。因此，将 n 和 n - 1 与运算总是能把 n 中最低位的 1 变成 0 ，并保持其他位不变。

使用这个小技巧，代码变得非常简单。

  • 时间复杂度：O(1)。运行时间依赖于数字 n 的位数。本题中是一个32位数字，因此时间复杂度位为 O(1)。
  • 空间复杂度：O(1)，没有使用额外的空间。

Method

  • Java
1
2
3
4
5
6
7
8
9
10
11
public class Solution {
    // you need to treat n as an unsigned value
    public int hammingWeight(int n) {
        int sum = 0;
        while(n!=0){
            sum++;
            n = n&(n-1);
        }
        return sum;
    }
}

Approach 3：字符串长度+正则匹配

Analysic

JS中，toString(radix) 方法可以将数字转换为基于 radix 的进制数（若 radix 缺省，则默认转换为 10 进制数）。

  • 首先，使用 toString(2) 方法，将数字转换为 2 进制字符串
  • 然后，使用正则匹配，滤除字符串中的 0，得到新的字符串
  • 最后，新字符串的长度即数字中 1 的个数

Solution

  • JS
1
2
3
4
5
6
7
/**
 * @param {number} n - a positive integer
 * @return {number}
 */
var hammingWeight = function(n) {
    return n.toString(2).replace(/0/g,'').length; 
};

Approach 4：使用内置函数

Analysis

  • Java中，函数 Integer.bitCount() 可以返回数字中2进制格式下 1 的个数。

    The java.lang.Integer.bitCount() method returns the number of one-bits in the two’s complement binary representation of the specified int value i. This is sometimes referred to as the population count.

  • 类似的，C++内置的 __builtin_popcount() 函数也可以返回数字中2进制格式下 1 的个数。

Method

  • C++
1
2
3
4
5
6
class Solution {
public:
    int hammingWeight(uint32_t n) {
       return __builtin_popcount(n);        
    }
};
  • Java
1
2
3
4
5
6
public class Solution {
    // you need to treat n as an unsigned value
    public int hammingWeight(int n) {
        return Integer.bitCount(n);
    }
}

338. Counting Bits（比特位计数）

Description

Approach 1-Pop count

Analysis

本问题可以看做 LeetCode- 191. Number of 1 Bits 的后续。

191. Number of 1 Bits 问题中，计数了一个无符号整数的位，结果称为 pop count，或 汉明权重。

现在，我们先默认这个概念。假设我们有函数 int popcount(int x)，可以返回一个给定非负整数的位计数。我们只需要在 [0, num] 范围内循环并将结果存到一个列表中。

  • 时间复杂度：O(nk)。对于每个整数 x，我们需要 O(k) 次操作，其中 k 是 x 的位数。
  • 空间复杂度：O(n)。

Solution

  • Java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public int[] countBits(int num) {
        int[] ans = new int[num+1];
        for(int i=0;i<= num;i++){
            ans[i] = popCount(i);
        }
        return ans;  
    }
    private int popCount(int x) {
        int count = 0;
        while(x!=0){
            count++;
            x = x&(x-1);
        }
        return count;
    }
}
  • C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    vector<int> countBits(int num) {
        vector<int> res(num+1,0);
        for(int i=0;i<=num;i++){
            res[i] = popCount(i);
        }
        return res;
    }
private:
    int popCount(int num){
        int count = 0;
        while(num){
            count ++;
            num &= num-1;
        }
        return count;
    }
};

Approach 2-动态规划+最高有效位

Analysis

利用已有的计数结果来生成新的计数结果。

假设有一个整数

1
x = (1001011101)_2 = (605)_{10}

我们已经计算了从 0 到 x - 1 的全部结果。

我们知道，x 与 我们计算过的一个数只有一位之差

1
x' = (1011101)_2 = (93)_{10}

它们只在最高有效位上不同。

让我们以二进制形式检查 [0, 3] 的范围

1
2
3
4
5
6
7
8
9
10
11
(0) = (0)_2

(1) = (1)_2

(2) = (10)_2

(3) = (11)_2

(4) = (100)_2

(5) = (101)_2

可以看出， 2 和 3 的二进制形式可以通过给 0 和 1 的二进制形式在前面加上 1 来得到。因此，它们的 pop count 只相差 1。

类似的，我们可以使用 [0, 3] 作为蓝本来得到 [4, 7]，使用 [0, 7] 作为蓝本来得到 [8, 15]，即根据区间 [0, b) 的结果去产生区间 [b, 2b) 的结果，其中 b 为

1
b = 2^m > x （m=0,1,2...）

总之，对于 pop count P(x)，我们有以下的状态转移函数

1
P(x + b) = P(x) + 1, b = 2^m > x （m=0,1,2...）
  • 时间复杂度：O(n)。对每个整数 x，只需要常数时间。
  • 空间复杂度：O(n)。需要 O(n) 的空间来存储结果。

Solution

  • Java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public int[] countBits(int num) {
        int[] res = new int[num+1];
        int i=0,b=1; //边界条件
        while(b<=num){
            // generate [b, 2b) or [b, num) from [0, b)
            while(i<b && i+b <= num){
                res[i+b] = res[i]+1;
                i++;
            }
            i = 0;   // reset i
            b <<= 1; // b = 2b
        }
        return res;
    }
}

Approach 3-动态规划+最低有效位

Analysis

只要 x' 小于 x，且它们的 pop count 之间存在函数关系，就可以写出状态转移函数。

遵循上一方法的相同原则，我们还可以通过最低有效位来获得状态转移函数。

观察 x 和 x' = x / 2 的关系

1
2
3
x=(1001011101)_2=(605)_{10}

x' = (100101110)_2 = (302)_{10}

可以发现 x' 与 x 只有一位不同，这是因为 x' 可以看做 x 移除最低有效位的结果。

这样，我们就有了下面的状态转移函数

1
P(x) = P(x/2) + (x mod 2)

例如

1
2
3
4
5
6
7
P(0) = 0;            //00   边界条件
P(1) = P(0) + 1;     //001   000
P(2) = P(1) + 0;     //010   001
P(3) = P(1) + 1;     //011   001
P(4) = P(2) + 0;     //100   010 
P(5) = P(2) + 1;     //101   010
P(6) = P(3) + 1;     //110   011

Solution

  • Java
1
2
3
4
5
6
7
8
9
10
class Solution {
    public int[] countBits(int num) {
        int[] res = new int[num+1];
        res[0] = 0;  //边界条件
        for(int i=0;i<=num;i++){
            res[i] = res[i/2] + (i%2);
        }
        return res;
    }
}

409. Longest Palindrome（最长回文串）

Description

Approach 1-Map计数

Analysis

使用 Map 数据结构统计每个字符串出现的次数。遍历 Map 字典，回文串长度增加 2*(map[i]/2)。同时，对出现次数对2取模，若为1，表示回文串中有出现单次的字符，设置标志位 hasSingle = true，最后记得对出现次数加1。

  • 时间复杂度： O(n)，n为字符串的长度，至少遍历每个字符一次。
  • 空间复杂度： O(1)，需要开辟额外空间来计数，字母最多为26个。

Solution

  • C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int longestPalindrome(string s) {
        map<char,int> dataInfo;
        int count = 0;
        bool hasSingel = false;
        for(int i=0;i<s.length();i++){
            dataInfo[s[i]]++;
        }
        for(int i=0;i<dataInfo.size();i++){
            if(dataInfo[i]%2 !=0){
                hasSingel = true;
            }
            count += 2*(dataInfo[i]/2);   //处理 'CCC'情况
        }
        count = hasSingel? count+1:count;
        return count;
    }
};
  • Java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public int longestPalindrome(String s) {
        char[] chas = s.toCharArray();
        Map<Character, Integer> map = new HashMap<>();
        for (int i = 0; i < chas.length; i++) {
            map.put(chas[i], map.getOrDefault(chas[i], 0) + 1);
        }
        int result = 0;
        for (int cnt : map.values()) {
            result += cnt / 2 * 2;
            if (cnt % 2 == 1 && result % 2 == 0) {
                result++;
            }
        }
        return result;
    }
}

223. Rectangle Area（矩形面积）

Description

Approach 1-面积拆分求解

Analysis

  • 根据上图，可以确定计算的面积值为两个矩形面积的和再减去重合部分的面积，即 resultArea = recArea1 + recArea2 - repetitionArea
  • 重合部分定点坐标的确定
    • Bottom Left Point Coordinate: (max(A,E), max(B,F))
    • Top Right Point Coordinate: (min(C,G), min(D,H))
  • 易忽略点

    Due to the total bits of “int” is 32, we prefer to use “w2<=w1” to “(int) w2-w1” to judge the return value. The data of ”(int) w2-w1” may overflow the range of integer.(For example, w2>0 and w1<0)

Slove

  • C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
	int computeArea(int A, int B, int C, int D, int E, int F, int G, int H)
	{
		int area_1 = (C - A)*(D - B);
		int area_2 = (G - E)*(H - F);
		//Calculate the overlap area
		int w1 = max(A, E);
		int h1 = max(B, F);
		int w2 = min(C, G);
		int h2 = min(D, H);
	
		if ((w2<=w1) || (h2<=h1)) //没有重合部分
		{
			return area_1 + area_2;
		}
		else
		{
			return area_1 + area_2 - ((h2-h1)*(w2-w1));
		}
	}
};

在计算过程上进行优化，有如下代码实现

1
2
3
4
5
6
7
8
class Solution {
public:
    int computeArea(int A, int B, int C, int D, int E, int F, int G, int H) {
        int left = max(A,E), right = max(min(C,G), left);
        int bottom = max(B,F), top = max(min(D,H), bottom);
        return (C-A)*(D-B) - (right-left)*(top-bottom) + (G-E)*(H-F);
    }
};
  • JS
1
2
3
4
5
var computeArea = function(A, B, C, D, E, F, G, H) {
    var left = Math.max(A,E), right = Math.max(Math.min(C,G), left);
    var bottom = Math.max(B,F), top = Math.max(Math.min(D,H), bottom);
    return (C-A)*(D-B) - (right-left)*(top-bottom) + (G-E)*(H-F);
};
  • Java
1
2
3
4
5
6
7
public class Solution {
    public int computeArea(int A, int B, int C, int D, int E, int F, int G, int H) {
        int left = Math.max(A,E), right = Math.max(Math.min(C,G), left);
        int bottom = Math.max(B,F), top = Math.max(Math.min(D,H), bottom);
        return (C-A)*(D-B) - (right-left)*(top-bottom) + (G-E)*(H-F);
    }
}

476. Number Complement (数字的补数)

Description

给定一个正整数，输出它的补数。补数是对该数的二进制表示取反。

注意

1. 给定的整数保证在32位带符号整数的范围内。
2. 你可以假定二进制数不包含前导零位。

示例 1

输入: 5
输出: 2
解释: 5的二进制表示为101（没有前导零位），其补数为010。所以你需要输出2。

示例 2

输入: 1
输出: 0
解释: 1的二进制表示为1（没有前导零位），其补数为0。所以你需要输出0。

Approach 1-寻找最高位为1的位置

Analysis

分析题目可知，只需对每个位的二进制数值（没有前导零位时）进行翻转即可。

但数值实际存储中，是包含前导零位的。如果直接对 num 进行取反操作，会把符号位取反，并且把最高位为 1 之前的所有位数都取反。

1
2
不含前导零位时，5 = 101，取反操作得到010，即十进制数值2
含有前导零位时（次数以8位为例），5 = 0000,0101，取反操作得到1111,1010

因此，对每位翻转（或取反，或和1进行异或）的起始位置是从最高位的1开始的，前面的 0 是不能被翻转的。可以考虑从高位往低位遍历，当遇到第1个1后，记录最高位为1的位置，之后再进行翻转操作（异或实现）。

Solution

  • C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int findComplement(int num) {
        if(num<=0) return num;
        int highestOneBit = 0; //最高位1的位数
        int tmp = num;
        while(tmp>0){
            highestOneBit += 1;
            tmp >>=1;
        }
        for(int i=highestOneBit-1;i>=0;i--){
            num = num ^(1<<i);  //异或操作
        }
        return num;
    }
};

Approach 2-创建每位都是1的二进制数值

Analysis

在不含前导零位时，把 num 和同位数的且每位都是1的二进制数进行与操作，即可得到结果。

因此，问题转化为求解一个和 num 位数一样且每位都是1的二进制数值 mask，最后进行异或操作（mask ^ num）即可。

例如，5 = 101，因此 mask = 111，进行异或操作 mask ^ num = 111 ^ 101 = 010。

得到每位都是1的二进制，如 111，可以通过1000 减去 1 得到。

Solution

  • Java
1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
    public int findComplement(int num) {
        int temp = num;
        int mask = 1;
        while(temp>0){
            mask <<= 1;
            temp >>= 1;
        }
        mask -= 1;   //1000-1 得到111
        return mask ^ num;  //异或
    }
}

Approach 3-转换为字符串+正则匹配

Analysis

此处给出JS实现的特解

  1. 先将 num 转化为二进制字符串
  2. 借助正则表达式查找，将字符串中的 0 替换成1
  3. 再将该字符串值转化成整数 int
  4. 最后将该值和 num进行异或操作

Solution

  • JS
1
2
3
4
5
6
7
8
/**
 * @param {number} num
 * @return {number}
 */
var findComplement = function(num) {
    var str = num.toString(2).replace(/0/g,1);  //转换为11..11
    return (num) ^ parseInt(str,2);
};