Do one thing at a time and do well

0%

LeetCode题解-001

发表于 更新于 分类于 阅读次数： Disqus：
  • 记录LeetCode题目笔记，汇总LeetCode解答记录

Overview

141. Linked List Cycle（环形链表）

Description

Approach 1-Hash Table

Analysis

  • 使用哈希表解决，时间复杂度为 O(n)，空间复杂度为 O(n)。
  • 遍历链表，若遇到 Null，则 表明链表无环。若遍历的节点在哈希表中已存在，则表明链表有环。

Solution

  • JavaScript
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */

/**
 * @param {ListNode} head
 * @return {boolean}
 */
var hasCycle = function(head) {
    let nodesSeen = new Set();
    if(head === null  || head.next === null){
        return false;
    }
    while(head !== null){
        if(nodesSeen.has(head)){
            return true;
        }
        else{
            nodesSeen.add(head);
        }
        head = head.next;
    }
    return false;
};
  • Java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */

public boolean hasCycle(ListNode head) {
    Set<ListNode> nodesSeen = new HashSet<>();
    while (head != null) {
        if (nodesSeen.contains(head)) {
            return true;
        } else {
            nodesSeen.add(head);
        }
        head = head.next;
    }
    return false;
}

Approach 2-Two Pointers

Analysis

  • 使用快慢指针解决，时间复杂度为 O(n)，空间复杂度为 O(1)。
  • Use two pointers, walker and runner.
  • Walker moves step by step.
  • Runner moves two steps at time.
  • If the Linked List has a cycle walker and runner will meet at some point.
  • Ref

Solution

  • C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    bool hasCycle(ListNode *head) {
        if(head == NULL){
            return false;
        }
        ListNode *walker = head; //moves one step each time
        ListNode *runner = head; //moves two step each time
        while(runner->next != NULL && runner->next->next != NULL){
            walker = walker->next;
            runner = runner->next->next;
            if(walker == runner){
                return true;
            }
        }
        return false;
    }
};
  • JavaScript
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */

/**
 * @param {ListNode} head
 * @return {boolean}
 */
var hasCycle = function(head) {
    if(head === null) {
        return false;
    }
    var walker = new ListNode();
    var runner = new ListNode();
    walker = head;
    runner = head;
    while(runner.next!==null && runner.next.next!==null) {
        walker = walker.next;
        runner = runner.next.next;
        if(walker === runner) return true;
    }
    return false;
};
  • Java 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public boolean hasCycle(ListNode head) {
        if (head == null || head.next == null) {
            return false;
        }
        ListNode slow = head;
        ListNode fast = head.next;
        while (slow != fast) {
            if (fast == null || fast.next == null) {
                return false;
            }
            slow = slow.next;
            fast = fast.next.next;
        }
        return true;
    }
}
  • Python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# Definition for singly-linked list.
# class ListNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution(object):
    def hasCycle(self, head):
        """
        :type head: ListNode
        :rtype: bool
        """
        if head == None or head.next == None:
            return False
        slow = fast = head
        while fast and fast.next:
            slow = slow.next
            fast = fast.next.next
            if slow == fast:
                return True
        return False

142. Linked List Cycle II （环形链表II）

Description

Approach 1-Two Pointers

Analysis

LeetCode-141. Linked List Cycle 中，完成了链表是否有环的判断。在此基础上，本题实现对环起点的判断和环长度的计算。

下面结合 LeetCode 141/142 - Linked List Cycle | CNBlogs 参考链接，对环起点的判断和环长度的计算进行分析。

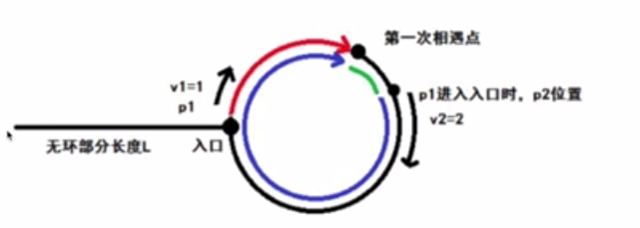
leetcode-142.png

设链表起点距离环的起点距离为a，圈长为n，当 walker 和 runner 相遇时，相遇点距离环起点距离为b，此时 runner 已绕环走了k圈，则

  • walker 走的距离为 a+b，步数为 a+b
  • runner 速度为 walker 的两倍，runner 走的距离为 2*(a+b)，步数为 a+b
  • runner 走的距离为 a+b+k*n=2*(a+b)，从而 a+b=k*n，a=k*n-b
  • 因此有，当 walker 走 a 步，runner 走 (k*n-b) 步。当 k=1 时，则为 (n-b) 步
环的起点

令 walker 返回链表初始头结点，runner 仍在相遇点。此时，令 walker 和 runner 每次都走一步距离。当 walker 和 runner 相遇时，二者所在位置即环的起点。

证明过程如下。

walker 走 a 步，到达环的起点；runner 初始位置为 2(a+b)，走了 a 步之后，即 kn-b 步之后，所在位置为 2(a+b)+kn-b=2a+b+kn= a+(a+b)+kn=a+2kn。因此，runner 位置是环的起点。

1
2
3
4
5
// runner走的位置
2(a+b) + a
= 3a + 2b    //消去b  b = k*n - a
= 3a + 2*(k*n - a)
= a + 2kn
环的长度

在上述判断环的起点的基础上，求解环的长度。

  • 当 walker 和 runner 相遇时，二者所在位置即环的起点。此后，再让 walker 每次运动一步。
  • walker 走 n 步之后，walker 和 runner 再次相遇。walker 所走的步数即是环的长度。

Solution

注意，在 while() 中需要使用 break 及时跳出循环，否则提交时会出现超时错误 Time Limit Exceeded

  • C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
       if(head == NULL){
            return NULL;
        }
        bool hasCycle = false;
        ListNode *walker = head; //moves one step each time
        ListNode *runner = head; //moves two step each time
        while(runner->next != NULL && runner->next->next != NULL){
            walker = walker->next;
            runner = runner->next->next;
            if(walker == runner){
                hasCycle = true;
                break;  //跳出循环
            }
        }
        if(hasCycle == true){
            walker = head;
            while(walker != runner){
                walker = walker->next;
                runner = runner->next;
            }
            return walker;
        }
        return NULL;
        
    }
};
  • JavaScript
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */

/**
 * @param {ListNode} head
 * @return {ListNode}
 */
var detectCycle = function(head) {
    if(head === null || head.next === null){
        return null;
    }
    // Tip - new ListNode() 创建可省略，节省代码运行时间
    // let walker = new ListNode();   // one steps
    // let runner = new ListNode();   // two steps
    let walker = head;
    let runner = head;
    let hasCycle = false;
    while(runner.next !== null && runner.next.next !== null){
        runner = runner.next.next;
        walker = walker.next;
        if(runner === walker){
            hasCycle = true;
            break; //jump loop
        }
    }
    if(hasCycle){
        walker = head;
        while(walker !== runner){
            runner = runner.next;
            walker = walker.next;
        }
        return walker;
    }
    return null;
};
  • Java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public ListNode detectCycle(ListNode head) {
        if(head == null || head.next == null){
            return null;
        }
        ListNode walker = head;
        ListNode runner = head;
        boolean hasCycle = false;
        while(runner.next != null && runner.next.next != null){
            walker = walker.next;
            runner = runner.next.next;
            if(walker == runner){
                hasCycle = true;
                break; //jump loop
            }
        }
        if(hasCycle){
            walker = head;
            while(walker != runner){
                walker = walker.next;
                runner = runner.next;
            }
            return walker;
        }
        return null;
    }
 
}
  • Python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
# Definition for singly-linked list.
# class ListNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution(object):
    def detectCycle(self, head):
        """
        :type head: ListNode
        :rtype: ListNode
        """
        if head == None or head.next == None:
            return None
        runner = walker = head
        hasCycle = False
        while runner and runner.next:
            runner = runner.next.next
            walker = walker.next
            if runner == walker:
                hasCycle = True
                break
        if hasCycle:
            walker = head
            while walker != runner:
                walker = walker.next
                runner = runner.next
            return walker
        return None

258. Add Digits（各位相加）

Description

Approach 1-Digit Root 公式

Analysis

将一正整数的各个位数相加(即横向相加)后，若加完后的值大于等于10的话，则继续将各位数进行横向相加直到其值小于十为止所得到的数，即为数根 (Digit Root)

本题目为求解一个非负整数的数根。参考 Digit Root | Wikipedia 可以了解数根的公式求解方法。

从上图总结规律，对于一个 b 进制的数字 (此处针对十进制数，b=10)，其 数字根 （digit root） 可以表达为

1
2
3
4
5
dr(n) = 0 if n == 0    

dr(n) = (b-1) if n != 0 and n % (b-1) == 0  // 9的倍数且不为零，数根为9

dr(n) = n mod (b-1) if n % (b-1) != 0  // 不是9的倍数且不为零，数根为对9取模

或者

1
dr(n) = 1 + (n - 1) % 9

Solution

  • C++
1
2
3
4
5
6
7
8
class Solution 
{
public:
    int addDigits(int num) 
    {
        return 1 + (num - 1) % 9;
    }
};
  • JavaScript
1
2
3
4
5
6
7
/**
 * @param {number} num
 * @return {number}
 */
var addDigits = function(num) {
    return 1 + (num - 1) % 9;
};
  • Java
1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
    public int addDigits(int num) {
        if (num == 0){
            return 0;
        }
        if (num % 9 == 0){
            return 9;
        }
        else {
            return num % 9;
        }
    }
}
  • Python
1
2
3
4
5
6
7
8
9
class Solution:
    def addDigits(self, num: int) -> int:
        """
        :type num:int
        :rtype :int
        """
        if num == 0: return 0
        elif num%9 == 0: return 9
        else: return num%9

461. Hamming Distance（汉明距离）

Description

Approach 1-异或位运算

对输入参数进行异或位运算得到一个二进制数值，再计算其中的数字 1 的个数即可。

在代码实现中，可以结合语言内置的API或方法，简化求解过程。

Analysis

  • JavaScript
1
2
3
4
5
6
7
8
9
10
11
12
13
/**
 * @param {number} x
 * @param {number} y
 * @return {number}
 */
var hammingDistance = function(x, y) {
    let xor = x^y;
    let total = 0;
    for(let i=0;i<32;i++){   // Number型 占32位
        total += (xor>>i) &1;
    }
    return total;
};

由于 Number 型占 32 位，因此，需要异或的结果进行32次移位，循环判断其中的数字 1 的个数。

下面考虑简化上述求解过程。

  1. number.toString(radix) 方法可以将一个数字以 radix 进制格式转换为字符串。可以将异或结果转换为 2 进制字符串。
  2. 对上述 2 进制字符串，使用正则表达式，只保留其中 1，将 0 替换为空。
  3. 最后，计算所得字符串的长度，即所求结果。
1
2
3
4
5
6
7
8
/**
 * @param {number} x
 * @param {number} y
 * @return {number}
 */
var hammingDistance = function(x, y) {
     return (x ^ y).toString(2).replace(/0/g, '').length;
};
  • Java

Java中，Integer.bitCount() 函数可以返回输入参数对应二进制格式数值中数字 1 的个数。

1
2
3
4
5
public class Solution {
    public int hammingDistance(int x, int y) {
        return Integer.bitCount(x^y);  //XOR
    }
}
  • C++

C++ 中, int __builtin_popcount 函数可以返回输入参数对应二进制格式数值中数字 1 的个数。

1
2
3
4
5
6
class Solution {
public:
    int hammingDistance(int x, int y) {
        return __builtin_popcount(x^y);
    }
};

463. Island Perimeter（岛屿的周长）

Description

Approach 1

Analysis

  • 遍历矩阵，找出 岛屿 islands 个数。若不考虑岛屿的周围，则对应的周长为 4 * islands
  • 对于岛屿，考虑其是否有左侧和顶部的邻居岛屿 neighbours。为了简化求解，对于所有岛屿，只考虑其左侧和顶部的邻居情况。
  • 综上，最终所求的周长为 4 * islands - 2 * neighbours

Solution

  • Java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public class Solution {
    public int islandPerimeter(int[][] grid) {
        int islands = 0, neighbours = 0;

        for (int i = 0; i < grid.length; i++) {
            for (int j = 0; j < grid[i].length; j++) {
                if (grid[i][j] == 1) {
                    islands++; // count islands
                    if (i !=0 && grid[i - 1][j] == 1) neighbours++; // count top neighbours
                    if (j !=0 && grid[i][j - 1] == 1) neighbours++; // count left neighbours
                }
            }
        }

        return islands * 4 - neighbours * 2;
    }
}
  • C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int islandPerimeter(vector<vector<int>>& grid) {
    	int count = 0, repeat = 0;
    	for (int i = 0; i<grid.size(); i++)
    	{
    		for (int j = 0; j<grid[i].size(); j++)
    		{
    			if (grid[i][j] == 1)
    			{
    				count++;
    				if (i!= 0 && grid[i-1][j] == 1) repeat++;
    				if (j!= 0 && grid[i][j - 1] == 1) repeat++;
    			}
    		}
    	}
    	return 4 * count - repeat * 2;
    }
};
  • JavaScript
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/**
 * @param {number[][]} grid
 * @return {number}
 */
var islandPerimeter = function(grid) {
    var count=0;
    var repeat=0;
    for(var i=0;i<grid.length;i++){
        for(var j=0;j<grid[i].length;j++){
            if(grid[i][j] === 1){
                count++;
                if((i!==0) && (grid[i-1][j]===1)){
                    repeat++;
                }
                if((j!==0) && (grid[i][j-1]===1)){
                    repeat++;
                }
            }
        }
    }
    return 4*count-2*repeat;
};