Do one thing at a time and do well

0%

动态规划经典题目整理

发表于 更新于 分类于 阅读次数： Disqus：
  • 记录和汇总动态规划经典题目

买苹果

Description

  • 动态规划-买苹果 | 牛客网
  • 小易去附近的商店买苹果，奸诈的商贩使用了捆绑交易，只提供 6 个每袋和 8 个每袋的包装(包装不可拆分)。 可是小易现在只想购买恰好 n 个苹果，小易想购买尽量少的袋数方便携带。如果不能购买恰好 n 个苹果，小易将不会购买。
  • 输入描述: 输入一个整数n，表示小易想购买 n(1 ≤ n ≤ 100) 个苹果
  • 输出描述: 输出一个整数表示最少需要购买的袋数，如果不能买恰好 n 个苹果则输出 -1
  • 测试用例
1
2
3
4
//input
20
//output
3

Approach 1-动态规划（通解）

Analysis

  • 采用动态规划方法求解。
  • 创建一个 vector 容器 steps，steps[i] 表示购买 i 个苹果所需的最小袋数。
  • 初始化为 steps 容器为 INT_MAX。
  • 从购买1个苹果开始遍历，若 steps[i] 为 INT_MAX，表示无法购买该个数的苹果，直接开始下次循环。
  • 若 steps[i] 不为 INT_MAX，表示该个数的苹果可以购买，进行动态规划求解。
  • 动态规划的转移方程为
1
2
steps[i+j] = min(steps[i]+1,steps[i+j])   //j为6或8
steps[0] = 0
  • 动态规划的过程如下图所示

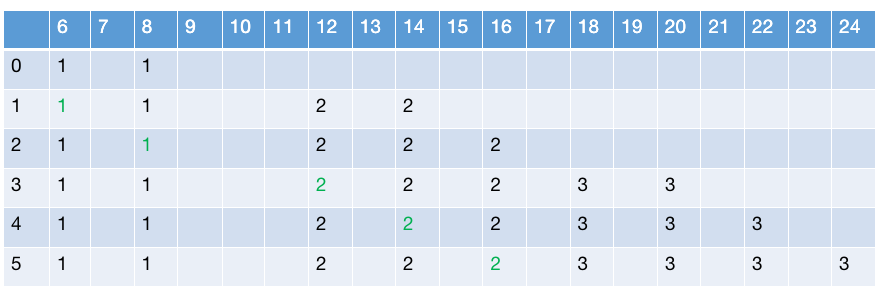
nowcode-buy-apple-1.png

Solution

  • C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include <iostream>
#include <vector>
#include <algorithm>
#include <climits>
using namespace std;

int main(){
    int amounts;
    cin>>amounts;
    //小于6情况处理
    if(amounts < 6){
        cout<<-1<<endl;
    }
    vector<int> steps(amounts+1,INT_MAX);
    steps[6] = 1;
    steps[8] = 1;
    for(int i=6;i<=amounts;i++){
        if(steps[i] == INT_MAX){
            continue;
        }
        else{
            if(i+6 <= amounts){
                steps[i+6] = min(steps[i]+1,steps[i+6]);
            }
            if(i+8 <= amounts){
                steps[i+8] = min(steps[i]+1,steps[i+8]);
            }

        }
    }
    steps[amounts] = (steps[amounts] == INT_MAX)? -1:steps[amounts];

    cout<<steps[amounts]<<endl;
    return 0;
}

Approach 2-贪婪算法

Analysis

  • 采用贪婪算法求解。
  • 优先选取每袋含有 8 个苹果的包装。若还有余数，则再用 6 个装的包装去购买。
  • 如果不行的话，则将 8 个装的个数减去 1 个，进行回溯，再用 6 包装的去购买。
  • 如果还不行的话，再次回溯，直到购买 8 包装的个数为 0。

贪婪算法并不一定能得到最优解，但是一个可行的，较好的解。 例如，给定硬币 coins=[1,2,10,25]，金额总数 amounts=30，不限制每种币值的硬币数量，要求用所给硬币凑出所需金额，并且硬币数量最少。若采用贪婪算法求解，需要 6 枚（25+5*1）硬币。 若采用动态规划求解，所需 3 枚（10+10+10）硬币。

下面对使用贪婪算法能否得到最优解进行分析。

  • 首先，6 和 8 都是偶数。因此，能凑出的个数也一定是偶数。程序中若苹果总数是奇数，可以直接返回 -1。
  • 再次，偶数个苹果数对 8 取模，其结果只可能为 0,2,4,6。
  • 若余数为 6 或者 0，则可以直接用 6 包装情况处理，不需要回溯购买 8 包装的情况。
  • 若余数为 4，只需回溯 1 次即可，因为8+4=12, 12%6=0。
  • 若余数为 2，只需回溯 2 次即可，因为8+8+2=18, 18%6=0。

综上，本题情况使用贪婪算法一定能得到最优解。

Solution

  • C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include <iostream>
using namespace std;

int maxPackages(int num) {
    int res = 0;
    int mul, remains;
    if(num%2 != 0){
        return -1;  //非偶数直接返回
    }

    if (num % 8 == 0) {
        res += num / 8;
        return res;
    }
    else{
        mul = num / 8;  //倍数
        remains = num % 8;
        res += mul;
        num = num % 8;
        while (mul >= 0) {  //回溯8包装
            if (num % 6 == 0) {
                res += num / 6;
                return res;
            }
            else {
                mul--;  //回溯  8包装购买袋数-1
                res--;
                num = num + 8;
            }
        }
    }
    return -1;

}

int main() {
    int num;
    while (cin >> num) {
        cout << maxPackages(num) << endl;
    }
    return 0;
}

Approach 3-数字分析求解

Analysis

  • 对数字特征进行分析。
  • 首先，6 和 8 都是偶数。因此，能凑出的个数也一定是偶数。程序中若苹果总数是奇数，可以直接返回-1。
  • 再次，偶数个苹果数对 8 取模，其结果只可能为 0,2,4,6。
  • 若余数为 6 或者 0，则可以直接用 6 包装情况处理，不需要回溯购买 8 包装的情况。
  • 若余数为 4，只需回溯 1 次即可，因为 8+4=12, 12%6=0。
  • 若余数为 2，只需回溯 2 次即可，因为 8+8+2=18, 18%6=0。

综上，可以采用如下思路进行处理。（由于数字 6 和 8 的特征，本方法只适用于本题，不具有通用性，动态规划为本题通用解法）

  • 情况1：若 num 不是偶数，则直接返回 -1
  • 情况2：若 num%8=0，则返回 num/8
  • 情况3：若 num%8 !=0，则只需回溯 1 次或者 2 次 8 包装购买个数，就可以求解。
    • 回溯 1 次，其结果为 n/8-1+2= n/8+1
    • 回溯 2 次，其结果为 n/8-2+3 = n/8+1
    • 因此，可以情况3下，可以返回 n/8+1

Solution

  • C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include <iostream>
using namespace std;

int main() {
    int num;
    while (cin >> num) {
        if(num%2 != 0){
            cout<<-1<<endl;
        }
        else{
            if(num%8 == 0){
                cout<<num/8<<endl;
            }
            else{
                cout<<1+num/8<<endl;
            }
        }
    }
    return 0;
}

跳石板

题目描述

小易来到了一条石板路前，每块石板上从1挨着编号为：1、2、3…….

这条石板路要根据特殊的规则才能前进：对于小易当前所在的编号为K的石板，小易单次只能往前跳K的一个约数(不含1和K)步，即跳到K+X(X为K的一个非1和本身的约数)的位置。 小易当前处在编号为N的石板，他想跳到编号恰好为M的石板去，小易想知道最少需要跳跃几次可以到达。

  • 例如
1
2
N = 4，M = 24：
4->6->8->12->18->24

于是小易最少需要跳跃5次，就可以从4号石板跳到24号石板。

  • 输入描述
1
输入为一行，有两个整数N，M，以空格隔开。 (4 ≤ N ≤ 100000) (N ≤ M ≤ 100000)
  • 输出描述
1
输出小易最少需要跳跃的步数,如果不能到达输出-1
  • 测试用例
1
2
3
4
5
//输出
4 24

//输出
5

Approach 1-动态规划

Analysis

采用动态规划思想求解。创建一个 vector 容器 steps，steps[i] 表示到达 i 号石板所需的最小步数。

  • 初始化为 steps 容器为 INT_MAX。
  • 从序号 N 的石板开始逐个遍历，若 steps[i]为 INT_MAX，表示该点不可到达，直接开始下次循环。
  • 若 steps[i] 不为 INT_MAX，表示该点可以到达。

动态规划的转移方程为

1
2
3
4
5
steps[i] = INT_MAX    //初始化所有值为INT_MAX
//i为石板编号，j=1,2...M-1
// 若j为i的约数，则 steps[i+j] = steps[i]+1
steps[i+j] = min(steps[i]+1,steps[i+j])   
steps[N] = 0

Solution

下面给出代码实现

  • C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include <iostream>
#include <vector>
#include <climits>
#include <cmath>
#include <algorithm>
using namespace std;

int main(){
    int N,M;
    while(cin>>N>>M){
        vector<int> steps(M+1,INT_MAX);
        steps[N] = 0;
        for(int i=N;i<=M;i++){
            if(steps[i] == INT_MAX){
                continue;
            }
            for(int j=2;(j*j)<=i;j++){
                if(i%j == 0){
                    if(i+j <= M){
                        steps[i+j] = min(steps[i]+1,steps[i+j]);
                    }
                    //如果j是约数，那么(i/j)也是约数
                    if(i+(i/j) <= M){
                        steps[i+(i/j)] = min(steps[i]+1,steps[i+(i/j)]);
                    }

                }

            }
        }
        if(steps[M] == INT_MAX){
            steps[M] = -1;
        }
        cout<<steps[M]<<endl;
    }
    return 0;
}

此处给出一个常规的优化项说明，上述代码在判断 for 循环时，限制循环终止条件为 (j*j)<=i，对于大于 sqrt(i) 的约数，在同一个for循环中进行判断，即

1
2
3
4
5
6
7
8
9
10
11
for(int j=2;(j*j)<=i;j++){
    if(i%j == 0){
        if(i+j <= M){
          ...
        }
        //如果j是约数，那么(i/j)也是约数
        if(i+(i/j) <= M){
           ...
        }
    }
}

上述可以明显减少for循环次数，针对N=4，M=24的情况，上述代码会执行10次循环。如果使用下述代码，将会执行15次代码（在牛客网系统上，会被当做超时处理）

1
2
3
4
5
6
7
for(int j=2;j<i;j++){
    if(i%j == 0){
        if(i+j <= M){
          ...
        }
    }
}

Approach 2-贪婪算法

Analysis

(本题目，使用贪婪算法并不能AC，此处给出的贪婪算法，仅作为一个示例给出，用于分析贪婪算法的使用场景)

贪婪算法并不一定能得到最优解，但是一个可行的，较好的解。

该问题若采用贪婪算法求解，并不会得到最优解，只会得到一个可行的，较好的解。例如，下述程序中采用了贪婪算法求解。每次都选取最大的约数前进一步。若后续发生不可到达目标点，则进行回溯，取第2大的约数作为步进值。下述程序通过率为80%，并不能AC。例如，对于N=676, M=12948情况，贪婪算法求解为13步，而动态规划算法求解为10步。

贪婪算法并不一定能得到最优解，但是一个可行的，较好的解。例如，给定硬币coins=[1,2,10,25]，金额总数amounts=30，不限制每种币值的硬币数量，要求用所给硬币凑出所需金额，并且硬币数量最少。若采用贪婪算法求解，需要6枚（25+5*1）硬币。 若采用动态规划求解，所需3枚（10+10+10）硬币。 — 贪婪算法

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
// 程序通过率为80%，并不能AC
//对于N=676, M=12948情况，贪婪算法求解为13步，而动态规划算法求解为10步。
// 贪婪算法并不一定能得到最优解，但是一个可行的，较好的解。
#include <iostream>
using namespace std;

int stepSearch(int N, int M) {
    if (N > M) {
        return -1;
    }
    if (N == M) {
        return 0;
    }
    int res = 0;
    for (int i = 2; i<N; i++) {
        if (i*(N / i) == N) {
            res++;
            if (stepSearch(N + N/i, M) != -1) {
                res += stepSearch(N + N/i, M);
                return res;
            }
            else {
                res--;
            }
        }
    }
    return -1;
}

int main() {
    int N, M;
    while (cin >> N >> M) {
        cout << stepSearch(N, M) << endl;
    }
    return 0;
}